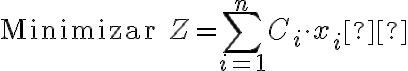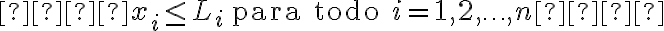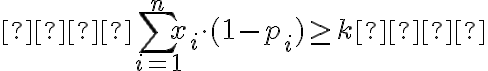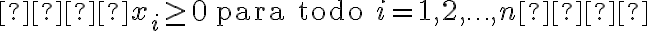Tema de Discusión

# Modelo de Optimización para la Distribución de Solicitudes entre Múltiples APIs

## Objetivo del Modelo

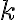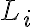Minimizar el costo total de procesamiento de $k$ solicitudes por minuto distribuyéndolas entre $n$ APIs, cada una con un límite de solicitudes por minuto $L_i$ y un costo por solicitud 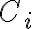$C_i$, considerando la probabilidad de fallo $p_i$.

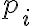## Variables de Decisión

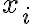- $x_i$: Cantidad de solicitudes enviadas a la API 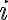$i$ en un minuto.

## Función Objetivo

Minimizar el costo total de las solicitudes enviadas:

$\text{Minimizar } Z = \sum_{i=1}^{n} C_i \cdot x_i$

donde:

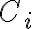- $C_i$ es el costo por solicitud enviada a la API $i$.

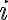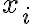- $x_i$ es la cantidad de solicitudes enviadas a la API $i$.

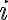## Restricciones

1. Límite de Solicitudes por API:

   $x_i \leq L_i \quad \text{para todo } i = 1, 2, \ldots, n$

   Esta restricción asegura que no se envíen más solicitudes a la API 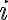$i$ de las que puede manejar por minuto ($L_i$).

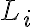2. Cumplimiento del Mínimo de Solicitudes (considerando la probabilidad de fallo):

   $\sum_{i=1}^{n} x_i \cdot (1 - p_i) \geq k$

   Esta restricción asegura que se procesen al menos 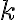$k$ solicitudes efectivas en total, considerando la probabilidad de fallo.

3. No Negatividad:

   $x_i \geq 0 \quad \text{para todo } i = 1, 2, \ldots, n$

   Esta restricción asegura que las cantidades de solicitudes enviadas sean no negativas.

## Descripción

- El objetivo es distribuir 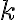$k$ solicitudes entre $n$ APIs de manera que el costo total sea mínimo, respetando los límites de cada API.

- Las 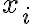$x_i$ se deben asignar de tal manera que se cumpla el mínimo de solicitudes 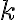$k$, sin exceder el límite 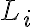$L_i$ de cada API.

- Este modelo puede ser resuelto utilizando técnicas de programación lineal, ya que tanto la función objetivo como las restricciones son lineales.

Lucas Ausquiz (5420454-3)
Antonio Parris (5034788-0)
Iván Gutiérrez (4879629-3)