Buenas
Esto es similar al ejercicio https://eva.fing.edu.uy/mod/forum/discuss.php?d=271232
La afirmación A es la definición de continuidad en 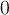 , sabiendo que
, sabiendo que 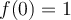 . Puedes ver tanto en la definición, como en el dibujo que la función
. Puedes ver tanto en la definición, como en el dibujo que la función  no es continua en 0.
no es continua en 0.
La afirmación D, lo que plantea es distinto. Voy a tratar de explicarlo de otra manera.
Sin importar cuales sean  , existe
, existe  que esta cerca de
que esta cerca de 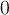 , sin ser
, sin ser 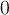 (es decir 0 < \vert x \vert < \delta) tal que
(es decir 0 < \vert x \vert < \delta) tal que 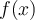 esta cerca de
esta cerca de  (es decir
(es decir  ). En el gráfico esto se ve
). En el gráfico esto se ve
Si quieres hacerlo de forma explicita, dados 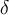 y
y 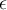 cualesquiera, el valor
cualesquiera, el valor  cumple la propiedad que se pide
cumple la propiedad que se pide
Saludos