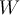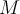Noviembre 2019 ejercicio 3 múltiple opción

Noviembre 2019 ejercicio 3 múltiple opción

de Angelo Valentin Pozzo Fripp -
Número de respuestas: 5

Hola, este ejercicio tiene como opción correcta la B, pero no entiendo porqué. A mi me piden el representante de riesz de T(S(abcd))=T(dbca)= d por definición. Entonces eso va a ser igual al producto interno entre la matriz (dbca) y una matriz W que es el representante de riesz. Es decir que T(S(A)) = <S(A),W> siendo A la matriz abcd. Operando según el PI que nos dan entonces yo llego a que el representante de riez me tiene que dar la matriz (1000).

Capaz estoy teniendo algún error,

Gracias.

En respuesta a Angelo Valentin Pozzo Fripp

Re: Noviembre 2019 ejercicio 3 múltiple opción

de Florencia Cubria -
No encontré dicho parcial Angelo, te pido que adjuntes la letra del ejercicio.

Saludos, Florencia.
En respuesta a Angelo Valentin Pozzo Fripp

Re: Noviembre 2019 ejercicio 3 múltiple opción

de Juan Piccini -
Hola Angelo, de lo visto en el teórico, si llamamos W al vector (matriz) que permite escribir (T\circ S)(V)=\langle V,W \rangle \;\forall\; V \in\mathcal{M}_{2\times 2} , tenemos que si B=\{E_1,E_2,E_3,E_4\} es una base ortonormal bajo el producto interno considerado, entonces W=(T \circ S)(E_1)E_1+\dots+(T \circ S ) (E_4)E_4 .
La base canónica es ortonormal para el producto interno que da la letra, y si haces las cuentas llegas a que W es la matriz de la opción B.
Saludos
J.
En respuesta a Juan Piccini

Re: Noviembre 2019 ejercicio 3 múltiple opción

de Angelo Valentin Pozzo Fripp -
Hola Juan, comprendo el razonamiento por ese lado, pero si lo hago por el método que usé yo, no entiendo porque no me da lo mismo ya que estoy cumpliendo con las hipótesis para hallar el representante.
Gracias
En respuesta a Angelo Valentin Pozzo Fripp

Re: Noviembre 2019 ejercicio 3 múltiple opción

de Florencia Cubria -
Hola Angelo, tu error es el siguiente: a ti te piden el representante de Riesz del funcional lineal T \circ S, esto es, el vector (en este caso, una matriz) M tal que T \circ S (A)  =T(S(A)) = \langle A,M \rangle y tu estás buscando el vector que verifique que (T \circ S) (A) = T(S(A)) = \langle S(A),M \rangle que no es lo mismo.

Dime si algo no se entendió.

Saludos, Florencia.