No logro entender por que la proyección se calcula así, llegue a la ecuación de arriba pero al calcular la proyección, dividi el vector del complemento de s por su norma e intente calcularlo haciendo <(1,-1,0),1/4(1,1,1)>1/4(1,1,1), lo cual no me lleva al resultado correcto.
Hola Santiago, recuerda que 
, de donde 
, de donde
Saludos
J.
Hola Juan, gracias por tu respuesta.
Tuve en cuenta esa igualdad, pero a la hora de calcular 𝑃𝑆⊥(𝑣) me queda igual a 1/16.(1,1,1). Esto porque normalice el vector de la base de 𝑆⊥ (1,1,1), quedándome 1/4(1,1,1), y luego usando esta igualdad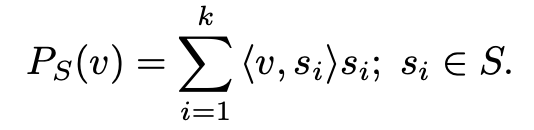
Tuve en cuenta esa igualdad, pero a la hora de calcular 𝑃𝑆⊥(𝑣) me queda igual a 1/16.(1,1,1). Esto porque normalice el vector de la base de 𝑆⊥ (1,1,1), quedándome 1/4(1,1,1), y luego usando esta igualdad
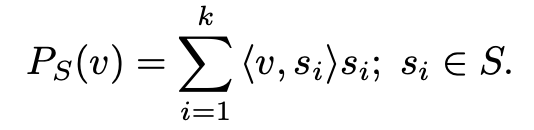
Entonces me queda que 𝑃𝑆⊥(𝑣) = <(1,-1,0),1/4(1,1,1)>1/4(1,1,1).
La diferencia que hay con la solución es que en el vector de la derecha usan (1,1,1), el cual no es ortonormal y no logro comprender por que se realiza el calculo así.
Ya encontre el error, estaba calculando el producto interno y no la norma, es 1/sqrt(4)