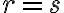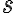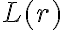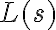Hola!
Se me esta complicando el manejo de las expresiones regulares para hacer pruebas del tipo L(r1) ⊆ L(r2) con r1 y r2 expresiones regulares.
Lei la prueba que subieron, pero para x ∈ L(ab)* es fácil ver que existe k tal que x = (ab)^k pero en el caso de expresiones regulares mas complejas como r1 = b.(a.b |b)* como se procede? vamos utilizando la def de L y separando el lenguaje en L(r1) = L(b) ∪ L(a.b|b)*.
En caso de aparecer mas de un exponente para representar una tira, sobre que se haría la inducción completa?
Dejo esta pregunta, porque es lo que mas me ha trancado al hacer ejercicios como el 4 o el 5. La intuición de por que representarían el mismo lenguaje la tengo, el problema es plasmarlo en la prueba.