TeoLeng: [Ejercicio 6] [Parte 5] Clausura de Kleene

Buenas tardes.

En un caso como en el de la imagen, se puede realizar esa igualdad? Sabiendo que el miembro derecho de la unión son combinaciones de tiras de L(r) y que estarán incluidas en la clausura del lenguaje

Re: Clausura de Kleene

de Santiago Gongora - miércoles, 16 de marzo de 2022, 16:54

Buenas tardes Cristian ¿cómo estás?

No me queda claro de dónde sale esa unión que estás intentando igualar a 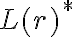$L(r)^*$ . Está bien que consideres que 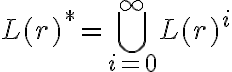$L(r)^* = \bigcup_{i=0}^{\infty} L(r)^i$ ya que es la definición de clausura de Kleene.

Si esto está enmarcado en el ejercicio 7)4) del práctico 1, te recomiendo que encares la prueba de 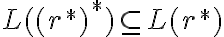$L((r^*)^*) \subseteq L(r^*)$ considerando una tira genérica 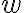$w$ perteneciente a la primera expresión. Entonces lo primero que vas a poder decir es:

$\exists k \in N: w \in L(r^*)^k \Longrightarrow w = w_1 w_2...w_k: (\forall i) i \in \{1...k\} \wedge w_i \in L(r^*)$

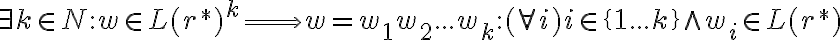
Una vez que hayas formulado a 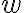$w$ de esa manera (como k subtiras pertenecientes a 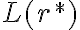$L(r^*)$ ) podés escribir análogamente cada una de las subtiras 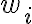$w_i$ con otro índice que no sea k.

Con eso vas a obtener una expresión para 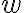$w$ donde no haya ninguna clausura de Kleene. Al visualizar la tira vas a poder encontrar un patrón que sea generado por 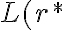$L(r^*$ ) y, como lo hiciste para una tira 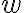$w$ genérica de 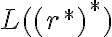$L((r^*)^*)$ , concluir la prueba.

Espero haya aclarado un poquito más el panorama :)

Saludos,
Santi

Re: Clausura de Kleene

de Cristian Gonzalez Nuñez - miércoles, 16 de marzo de 2022, 17:18

Anteriormente había encarado el ejercicio por el lado que explicás y ahora estaba probando si también podía sacarlo usando las definiciones de expresión regular y clausura de Kleene.

Al escribir el conjunto que define (r*)* obtengo una unión de uniones, y de esa unión de uniones, consigo la definición de la clausura de Kleene cuando i = 1. Mi pregunta era más bien si podía darse por hecho que el resto de conjuntos están incluidos en la clausura de L(r), puesto que son combinaciones del lenguaje

Re: Clausura de Kleene

de Santiago Gongora - miércoles, 16 de marzo de 2022, 17:35

Hola Cristian,

estuve comentando acá con Juanjo tu consulta. Si entendemos bien, lo que vos decís te sirve para probar que

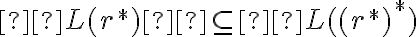$L(r^*) \subseteq L((r^*)^*)$ porque, como bien decís, es como si tomaras

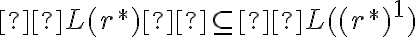$L(r^*) \subseteq L((r^*)^1)$ ya que, directamente,

$L(r^*) = L((r^*)^1) \Longleftrightarrow L(r^*) = L(r^*)$ .

Pero el otro sentido (

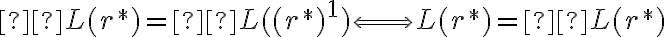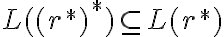$L((r^*)^*) \subseteq L(r^*)$ ) se complica para probarlo así. De todos modos, si querés mañana en la consulta podemos ver todo el planteo entero :D

Saludos,
Santi