Buenas, llego a la siguiente formula en este ejercicio pero no se como seguir con la demostración.
x pertenece a L(r1) si x= (0 l1)^m 0 1^n
y pertenece a L(r2) si y= 1^n' 0 (0 l1)^m´
Buenas, llego a la siguiente formula en este ejercicio pero no se como seguir con la demostración.
x pertenece a L(r1) si x= (0 l1)^m 0 1^n
y pertenece a L(r2) si y= 1^n' 0 (0 l1)^m´
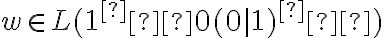 entonces tiene la forma
entonces tiene la forma 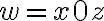 donde
donde 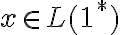 y
y 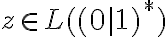 . Y de ahí podés empezar a transformar la expresión para llegar a algo que sepas que es generado por
. Y de ahí podés empezar a transformar la expresión para llegar a algo que sepas que es generado por 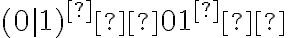 ...
...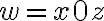 , donde
, donde 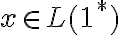 y llegamos a que
y llegamos a que 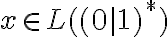 , que es exactamente lo que queremos, la primera parte del otro lenguaje, para llegar a que
, que es exactamente lo que queremos, la primera parte del otro lenguaje, para llegar a que 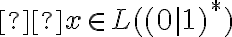 y
y 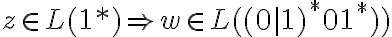
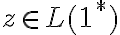 . partiendo de lo de santi, sabemos que
. partiendo de lo de santi, sabemos que 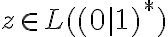 , y acá va otro pique, y es que podemos distinguir en casos, cuando z tiene 0's y cuando no. cuando no los tiene es trivial, en el caso que si los tenga podemos volver a proponer una tira genérica, en este caso fijando el último cero por ejemplo:
, y acá va otro pique, y es que podemos distinguir en casos, cuando z tiene 0's y cuando no. cuando no los tiene es trivial, en el caso que si los tenga podemos volver a proponer una tira genérica, en este caso fijando el último cero por ejemplo: 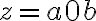 donde
donde 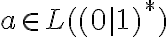 y
y 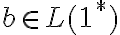 . con esto podes sustituir en el w original y ver cómo te queda la tira
. con esto podes sustituir en el w original y ver cómo te queda la tirahola:
no sé cómo efectivamente habrás planteado la demostración, pero por lo que decís, te diría que no se puede probar así... si yo tomo dos elementos cualesquiera de un mismo conjunto, no necesariamente son lo mismo.
otra cosa sería probar la doble inclusión, como sugieren santiago y belén, en cuyo caso el uso de inducción suele ser una manera más elegante (y rápida) de probar ciertas cosas, aunque no necesariamente el único camino para esa demostración.
saludos,
d.-