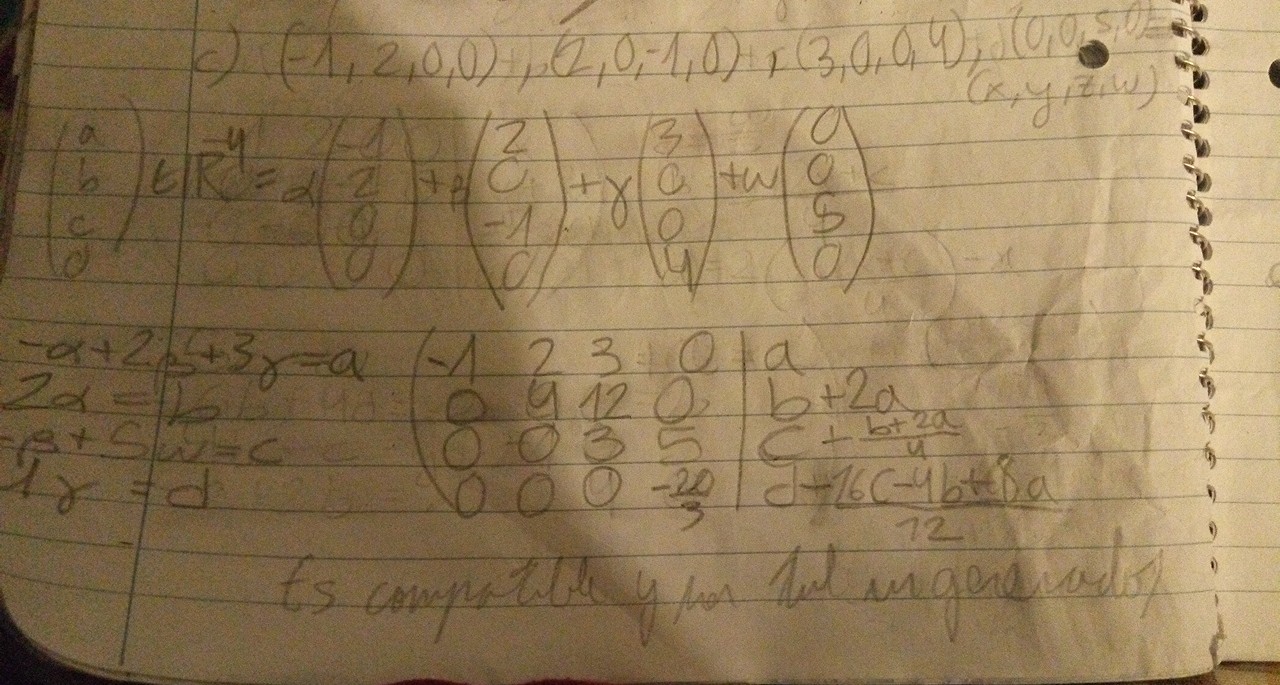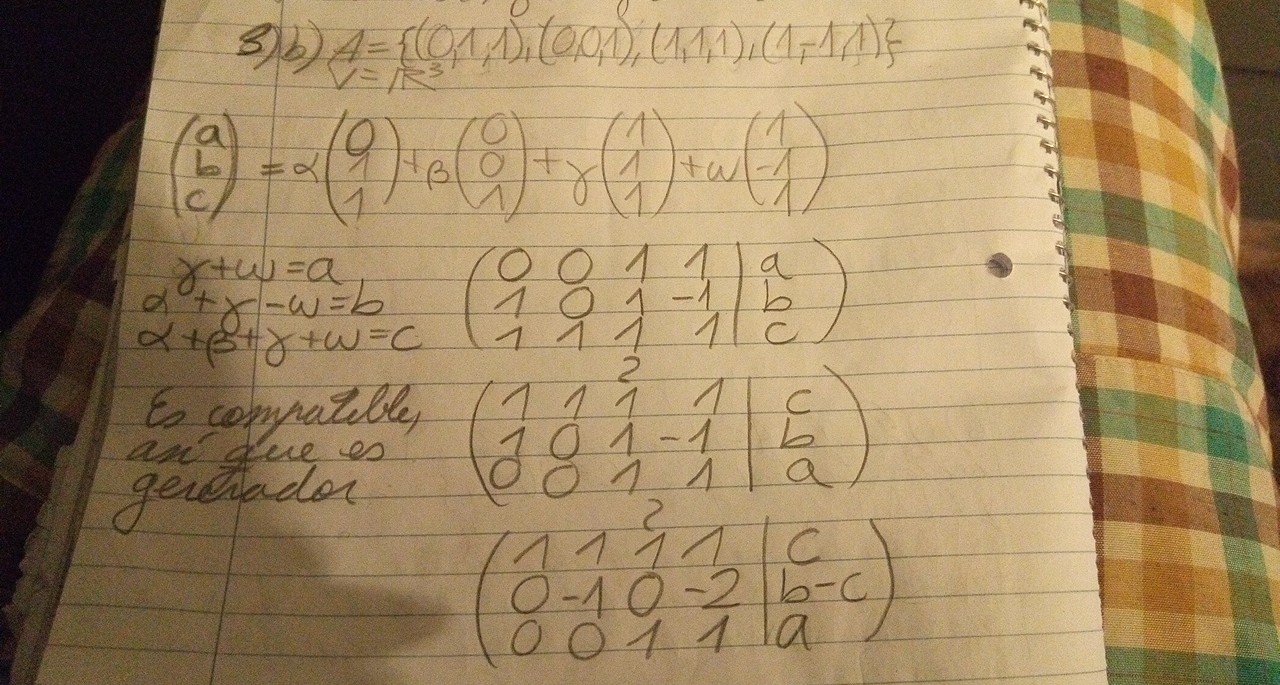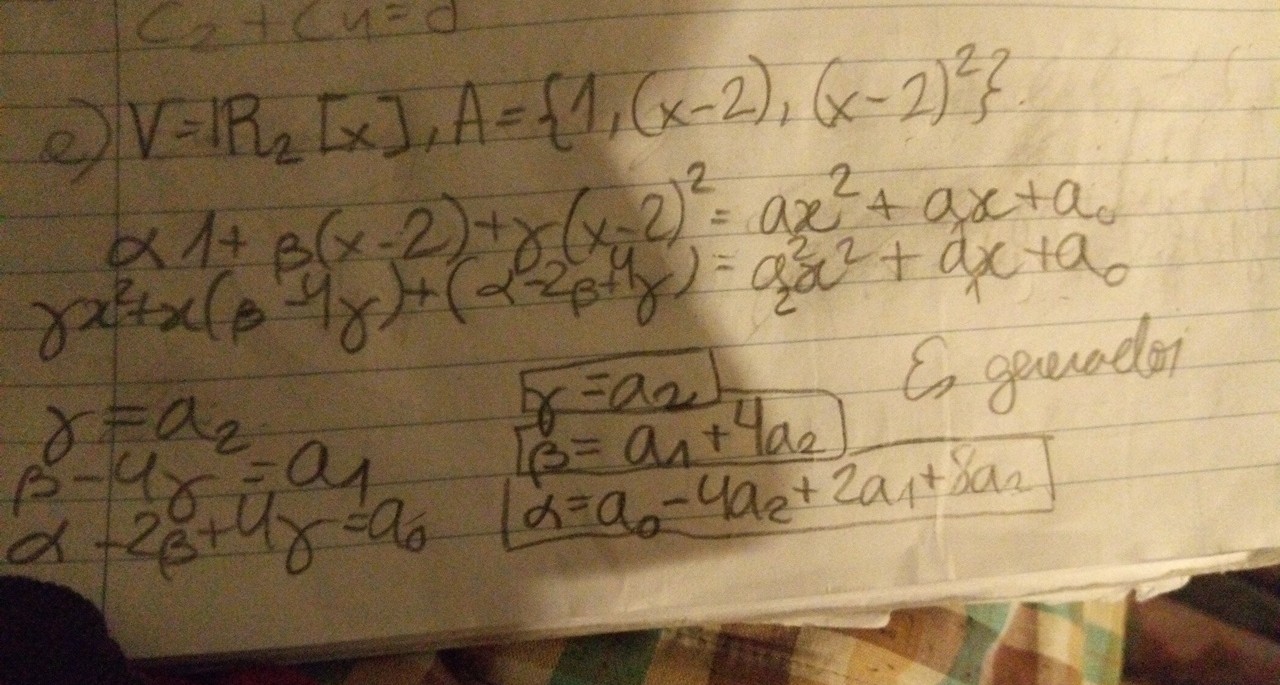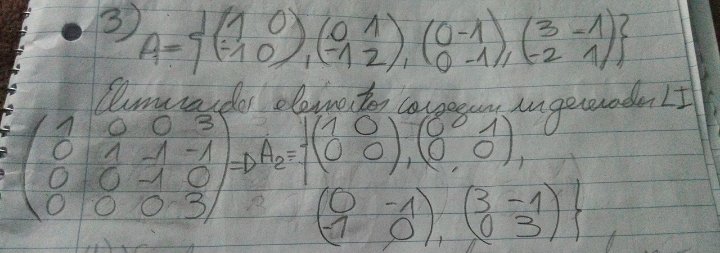Ejercicio 1

Ejercicio 1

de Nataly Melanie Ruber Maimo -
Número de respuestas: 9

Hola, era para saber si tenía bien razonado estos del 1;

en el a), sí es combinación lineal, lo averigüé sumando (1,2,1)+(3,-1,0)+(-1)(1,1,0) y me dio el (3,0,6)

b) Aquí yo agarré K1(1,3,2,1)+ K2(2,−2,−5,4)+ k3(2,−1,3,6) y lo igualé a (2,5,-4,0) y lo convertí en una matriz, sin embargo se podía ver que me iba a dar incompatible por el 0, no sé si éso es requisito para que no haya combinación lineal, pero si lo es, entonces aquí no hay.

c) Aquí no hay, probé algunas combinaciones, y probé sumar 3x 3 + x −2x 2 + x − 1 +3x 3 − 2x 2 + 2x − 1 y me dio -3x3+4x2+x-2, que no es digamos, múltiplo si se puede decir, del −3x 3 + 4x 2 + x − 2, o sea no hay manera que multiplicando me de eso. Así que yo creo que no es combinación lineal.


d) Esta sí, se ve sólo sumando


Luego, en la 3, en la que dice ,b) V = R3 , A = {(0,1,1),(0,0,1), (1,1,1), (1,−1,1)}., es válido decir que al haber 4 conjuntos en A, no puede ser R3? 

En respuesta a Nataly Melanie Ruber Maimo

Re: Ejercicio 1

de Bruno Dominguez -

Hola Nataly,

La idea es que todos los casos lo resuelvas planteado un sistema como hiciste en la parte b, y no solo a ojo xq puede haber más de una manera de llegar al mismo vector (como por ejemplo en la parte d). También cuidado en la parte b que el sistema sí da compatible. Luego en la parte c efectivamente no es compatible pero entiendo que llegaste tanteando y no es la idea.

Para todos los casos tenés que plantearte si $$\exists \lambda_1, \lambda_2, ..., \lambda_p \in \mathbb{R} / \lambda_1v_1+\lambda_2v_2 + ... + \lambda_pv_p=v $$ ?


Para el caso de $$\mathbb{R}^n$$ es claro cómo trabajar (lo que mencionaste en la parte b).


Cuando tenés polinomios, la idea es que reagrupes la ecuación que planteas por grado (todo lo multiplicado por $$x^n$$ por un lado, todo lo multiplicado por $$x^{n-1}$$ por otro, y así) y luego utilizando que para que dos polinomios sean iguales, sus coeficientes tienen que ser iguales, te armas un sistema de ecuaciones y resolvés.

Luego de que hagas esto un par de veces, vas a poder darte cuenta que hay una analogía entre $$\mathcal{P}_n$$ y $$\mathbb{R}^{n+1}$$, de forma tal que, por ejemplo, a un polinomio $$ax^2+bx+d \in \mathcal{P}_2$$ lo podes pensar como un vector $$(a,b,c) \in \mathbb{R}^3$$.


Luego, para las matrices es similar a $$\mathbb{R}^n$$ pensandolo entrada a entrada. Con la matrices también vas a poder encontrar una analogía entre las $$\mathcal{M}_{n\times n}$$ y $$\mathbb{R}^{n\times n}$$.


Con respecto al ej3, lo que planteas no es correcto. Que el conjunto $$A \subset \mathbb{R}^3$$ tenga 4 vectores a priori no implica que no puedas generar $$\mathbb{R}^3$$ con él. Lo que sí implica es que A es un conjunto linealmente dependiente (en este caso, al menos uno de los vectores va a ser combinación lineal de los otros), xq tenes 4 vectores en un espacio de 3 dimensiones. Para entender esto un poco mejor bajemos una dimensión y pensemos en un plano $$(\mathbb{R}^2)$$, para indicarte 1 punto del plano a partir de un punto de referencia solo preciso darte 2 vectores, cualquier otro vector que te de sería información extra que te la podría haber dicho con los primeros dos.


Cualquier cosa que no se entienda preguntá de nuevo,

Saludos
En respuesta a Bruno Dominguez

Re: Ejercicio 1

de Nataly Melanie Ruber Maimo -

Hola profe soy yo de nuevo, era solo para comprobar si el procedimiento que le hago a las cosas es el correcto ahora, más allá de si tengo algún error de cuenta xD te paso los que no tengo seguridad que estén 100% bien, porque capaz tengo mal el procedimiento


Este de acá creo que tengo algún error de cuenta porque me da un poco feo, mi idea en este de arriba es que puesto que es compatible, es generador.


Acá tengo la misma idea


Aquí tengo la idea de que la matriz para ser generadora no debe anularse en ningún sitio, porque sino no puede generar completamente, no se si me explico, acá puede ser que esté mal esa idea


Aquí me pareció que no era necesario una matriz porque lo veo ya escalerizado, y como es compatible, sería generador


Este me fijé si tenían el mismo alfa, beta y gamma, no se 100% si iba por ahí pero me pareció que sí


Este tengo duda si está bien el procedimiento, me parece que sí, pero por las dudas, lo que hice fue pensar que si queda dependiente, entonces al menos uno de ellos puede eliminarse entre sí y no es necesario que todos los "alfa", digamos, den 0, y como acá son independientes, sería necesario que para qué esto de 0, que los alfa todos den 0 (en este caso sería alfa ,beta y gamma), o sea apliqué la definición


Este no sé 100% si es correcto decir lo de a para los reales como respuesta a la pregunta de hallar un subconjunto con la mayor cantidad de elementos posible que sea linealmente independientes, pero me parece que tiene lógica, igual por las dudas lo paso



Luego, podrías darme un consejo para la 1)2)a)? Es la de S ={(x,y,z) ∈ R3: x+y+z =0} ., sé cómo se resuelven las otras dos pero esta no sé bien cómo hacerlo



Graciass

En respuesta a Nataly Melanie Ruber Maimo

Re: Ejercicio 1

de Bruno Dominguez -

Hola, vamos en orden.

Lo primero que planteas es correcto, si el sistema es compatible (determinado o indeterminado) el conjunto genera V. No me fijé las cuentas.

Lo de la matriz es correcto, pero para poder estar seguro tenés resolver el sistema que te quedó planteado para ver si te queda compatible o no (si no te queda compatible es que una de las entradas termina siendo nula).

El del polinomio está bien razonado, igual no siempre te va a quedar escalerizado de entrada y vas a tener que resolver el sistema.

En el 1.4 por como lo hiciste, lo que tenés que chequear en realidad es que la condición que se debe cumplir para que el sistema sea compatible (que es la condición que los vectores deben cumplir para pertenecer al espacio generado, es decir que sean combinación lineal de los vectores del conjunto) sea la misma. Cuando lo resolviste copiaste mal el primer vector del conjunto A1 en la matriz. Te dejo acá un post para que leas https://eva.fing.edu.uy/mod/forum/discuss.php?d=184642#p418280 y la solución escrita del semestre pasado https://eva.fing.edu.uy/pluginfile.php/294034/mod_resource/content/1/p9_GAL1_2020_Ej_1_4a.pdf.

En el 2, no entendí como llegaste al sistema que resolvés. El primer renglón es correcto, por lo tanto el sistema que te queda a resolver es \( \begin{cases} a \alpha - \beta=0 \\ a^2 \alpha + a \beta + 2a^2 \gamma =0 \\ \alpha + a \beta +(a^2+1)\gamma =0 \end{cases} \), pasado a matriz esto resulta igual a "colgar" los vectores del conjunto: \( \begin{pmatrix} a & -1 & 0 \\ a^2 & a & 2a^2 \\ 1 & a & a^2+1 \end{pmatrix} \), un detalle es que no agrego el término independiente xq como es todo cero siempre lo va a hacer y escribirlo no es necesario (igual si lo preferís, hacelo). Bueno, dado el sistema con los a, lo resolves y estudiando los diferentes casos según a ves cuando es LI (SCD) y cuando es LD (SCI), acordate que como es un sistema homogéneo compatible siempre va a ser.

En el último, la idea es que para los valores de $$a$$ que haga que el conjunto sea LD elimines vectores hasta hacerlo LI, o sea tenes que eliminar a los vectores que podes formar a partir de los demás. De forma genérica, siempre vas a poder eliminar un vector cuyo "alpha" (como los llamaste antes) NO sea cero, de forma práctica podes eliminar los vectores correspondientes a los que te queden en el "escalón largo" después de escalerizar, ya que estos no van a tener un alpha=0. Igual en lo que planteas sería $$A\ LI \ \forall a \in \mathbb{R} \backslash \{2\}$$ en vez de 4, no?


Y para el 1)2)a, la receta de este tipo de ejercicios es: 

1) A partir de la condición del subespacio, obtengo relación entre las variables 

2) Impongo relación en vector genérico del espacio vectorial

3) Desarrollo lo que me queda separando por variables, donde los vectores que te quedan son el generador de tu subespacio

Entonces quedaría: 

1) $$x+y+z=0 \implies x=-y-z$$

2)$$v=(x,y,z) \in S \iff v=(-y-z,y,z)$$

3) $$(-y-z,y,z)=(-y,y,0)+(-z,0,z)=y(-1,1,0)+z(-1,0,1) \implies \{ (-1,1,0),(-1,0,1) \} \text{ genera } S$$


Espero haya quedado claro, cualquier cosa preguntá de nuevo,

Saludos
En respuesta a Bruno Dominguez

Re: Ejercicio 1

de Nataly Melanie Ruber Maimo -
Hola, pude entender lo que explicabas, me quedaron algunas dudas pocas;

En el 2)a), donde hay dependencia lineal, y te preguntan un subconjunto LI que permita expresar a los otros dos como combinación lineal de él mismo está bien elegir al (1,0,1,2)? Porque resolviendo la matriz , es el que queda sin dependencia


Luego, en el 3) estaría bien así? 


Mi idea fue escalerizarlo, pero no noté dependencia entre los elementos, así que no sé qué falló


Gracias por la ayuda !!!

En respuesta a Nataly Melanie Ruber Maimo

Re: Ejercicio 1

de Bruno Dominguez -

Hola, no entendí cual es el 2)a) que te referís xq no encontré el vector (1,0,1,2) entre los vectores de los ejercicios. Cuando decís que queda sin dependencia, querés decir que su "alpha" es cero? Si es esto ese vector no lo podes eliminar. Explicame un poco más a cuál te referías y vemos.

Respecto al 3, la forma escalerizada a la que llegaste es correcta, por lo que el conjunto es LI y no tenés que hacerle nada. Por las dudas, la idea nunca es sustituir los vectores de tu conjunto por los que te quedan en la matriz escalerizada, los vectores de tu conjunto siempre son con los que empezaste, vos solo usas el sistema para estudiar su independencia lineal, y en caso de eliminar alguno también es de los que tiene tu conjunto dejando el resto.

Saludos


En respuesta a Bruno Dominguez

Re: Ejercicio 1

de Nataly Melanie Ruber Maimo -

Holi, de aquí saqué el (1,0,1,2)


Lo pensé como que ese (1,0,1,2) provoca que los otros dos queden en combinación lineal, pero capaz no le estoy acertando a lo que me están pidiendo

En respuesta a Nataly Melanie Ruber Maimo

Re: Ejercicio 1

de Bruno Dominguez -

Ah, ya entendí.  Ta no, las filas de la matriz no representan vectores, además fijate que el espacio que te dan es $$\mathbb{R}^3$$ y el vector que planteaste es de $$\mathbb{R}^4$$.

Si terminas de escalerizar la matriz esta te queda: \( \begin{pmatrix} 1 & 0 & 1 & 2 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 0 & 0 \end{pmatrix} \), es decir un SCI con 2 grados de libertad. Esto quiere decir que hay 2 vectores del conjunto que los podes formar como combinación del resto y que tenés que eliminar dos vectores para formar un conjunto LI. La dependencia de lineal de los vectores es la solución del sistema, la relación que hay entre los "alphas".

Como te puse más arriba, de forma genérica, siempre vas a poder eliminar un vector cuyo "alpha" NO sea cero, de forma práctica podes eliminar los vectores correspondientes a los que te queden en el "escalón largo" después de escalerizar, ya que estos no van a tener un alpha=0. Por lo tanto, de forma práctica para lograr un conjunto LI podes eliminar los vectores (1,1,1) y (2,3,4) que son los que corresponden al escalón largo (repito, no necesariamente tienen que ser estos, mientras su "alpha" no sea cero lo podes eliminar). Entonces tu nuevo conjunto LI quedaría $$A'= \{ (1,2,3) , (0,1,2) \}$$.

Saludos