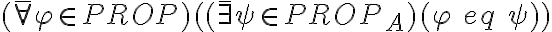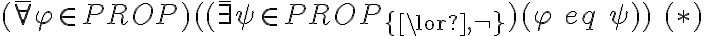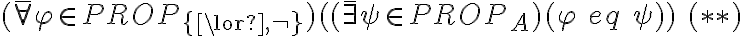Semántica de la lógica proposicional

Hola,

para probar que un conjunto 'A' de conectivos es completo, lo que deberías probar es:

$(\bar \forall \varphi \in PROP)((\bar \exists \psi \in PROP_{A})(\varphi\ eq\ \psi))$

Para facilitar esta tarea, podés utilizar conjuntos de conectivos que se sepa que son completos, por ejemplo, se sabe que:

$(\bar \forall \varphi \in PROP)((\bar \exists \psi \in PROP_{\lbrace \lor, \neg \rbrace})(\varphi\ eq\ \psi))\ (\ast)$

entonces para probar que 'A' es completo alcanza con probar:

$(\bar \forall \varphi \in PROP_{\lbrace \lor, \neg \rbrace})((\bar \exists \psi \in PROP_{A})(\varphi\ eq\ \psi))\ (\ast \ast)$

Observá que como sabemos que toda fórmula de 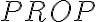$PROP$ se puede escribir en términos de 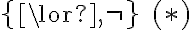$\lbrace \lor, \neg \rbrace\ (\ast)$, si logramos probar que toda fórmula de 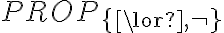$PROP_{\lbrace \lor, \neg \rbrace}$ se puede escribir en términos de los conectivos del conjunto 'A' 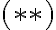$(\ast \ast)$, entonces estamos probando que podemos escribir toda fórmula de 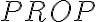$PROP$ en términos de los conectivos del conjunto 'A'.

Esto podrías aplicarlo para cualquier conjunto completo de conectivos.

Los equivalentes que encontraste los vas a usar adentro de la prueba para encontrar el 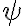$\psi$ equivalente para cada $\varphi$.

Si no quedó claro volvé a consultar.

Saludos!