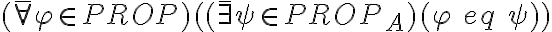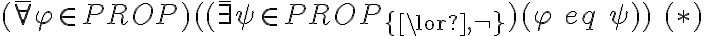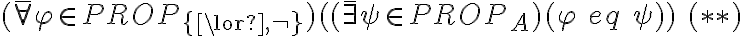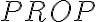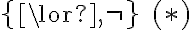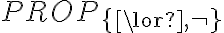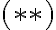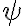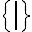Lógica_R: Práctico 3, ejercicio 9 a

Buenas! En este ejercicio se pide demostrar que

$\{|\}$ y

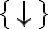$\{\downarrow\}$ son completos.
La manera directa de probar esto es encontrar equivalentes para cada conectivo de PROP en términos de

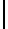$|$ y en términos de

$\donwarrow$ .
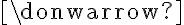Pero, por otro lado me doy cuenta que es posible encontrar un equivalente para cada uno de esos conectivos en términos de

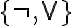$\{\neg,\vee\}$ , el cual por Teorema 1.3.6 es un conjunto completo.
Se puede concluir entonces, a partir de este Teorema, que

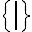$\{|\}$ y

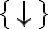$\{\downarrow\}$ son completos o necesariamente tengo que hacer lo primero que dije?

Muchas gracias!

Re: Práctico 3, ejercicio 9 a

de Camila Sanz - miércoles, 19 de abril de 2017, 10:30

Hola,

para probar que un conjunto 'A' de conectivos es completo, lo que deberías probar es:

$(\bar \forall \varphi \in PROP)((\bar \exists \psi \in PROP_{A})(\varphi\ eq\ \psi))$

Para facilitar esta tarea, podés utilizar conjuntos de conectivos que se sepa que son completos, por ejemplo, se sabe que:

$(\bar \forall \varphi \in PROP)((\bar \exists \psi \in PROP_{\lbrace \lor, \neg \rbrace})(\varphi\ eq\ \psi))\ (\ast)$

entonces para probar que 'A' es completo alcanza con probar:

$(\bar \forall \varphi \in PROP_{\lbrace \lor, \neg \rbrace})((\bar \exists \psi \in PROP_{A})(\varphi\ eq\ \psi))\ (\ast \ast)$

Observá que como sabemos que toda fórmula de $PROP$ se puede escribir en términos de $\lbrace \lor, \neg \rbrace\ (\ast)$ , si logramos probar que toda fórmula de $PROP_{\lbrace \lor, \neg \rbrace}$ se puede escribir en términos de los conectivos del conjunto 'A' $(\ast \ast)$ , entonces estamos probando que podemos escribir toda fórmula de $PROP$ en términos de los conectivos del conjunto 'A'.

Esto podrías aplicarlo para cualquier conjunto completo de conectivos.

Los equivalentes que encontraste los vas a usar adentro de la prueba para encontrar el $\psi$ equivalente para cada $\varphi$ .

Si no quedó claro volvé a consultar.

Saludos!