Revisando las notas de derivación me di cuenta que
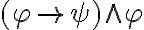 es muy parecido al modus ponen o regla de elminiación del implica, por lo que
es muy parecido al modus ponen o regla de elminiación del implica, por lo que 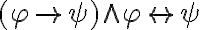 .
.Sin embargo no me cierran las cuentas por lo que concluyo que no son equivalentes. En que me estoy equivocando?
Hola.
Efectivamente no es equivalente. El problema es cómo sacas @#\varphi#@ en el recíproco.
Por otro lado, trabajando por equivalencias, se lleva bastante fácil a que esto debiera ser equivalente a @#\varphi \land \psi#@