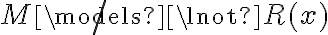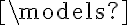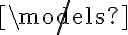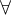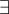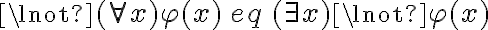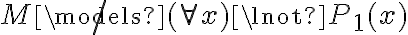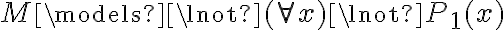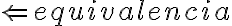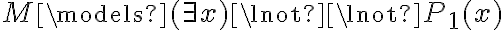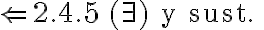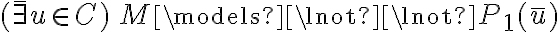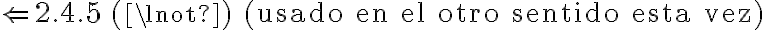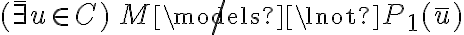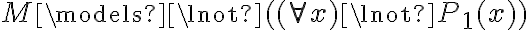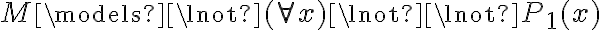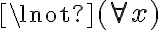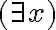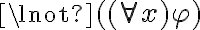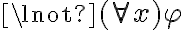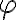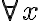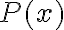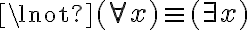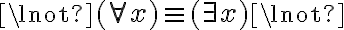Lógica: Examen Julio 2016 - Ejercicio 1

Buenas,

Parte c)
¿Puedo justificar que ac ¬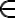 $\in$ L3 asi?:

Solo hace falta observar que la clausula inductiva III es la única en la cual aparece el carácter c, pero siempre precedido de una b (bc), por lo cual no es posible formar la cadena ac en L3.

Parte d)
Priemro, M=<C, R>, donde C es el conjunto y R es la relación, cuando plantean el enunciado M ¬|= ¬P₁(x), ¿No sería M ¬|= ¬R(x) ? Ya que todavía no pasamos al lenguaje de los símbolos.
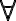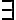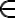Segundo, en la solución aparece lo siguiente: M ¬|= ¬P₁(x) ==(clausura)> M ¬|= (( $\forall$ x) ¬P₁(x) ==(2.4.5)> ( $\exists$ k) $\in$ C : M ¬|= ¬P₁(x). ¿Porque se saca el 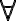$\forall$ como un 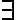$\exists$ ? ¿No es que si dice ¬ 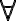$\forall$ puedo convertirlo y sacarlo en 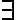$\exists$ ? En este caso sí hay un ¬|= el cual eventualmente se convierte en |= ¬( 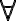$\forall$ ) y ahí si sale como el existe, pero ustedes en la solución sacan el existe sin sacar un ¬ 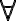$\forall$ , solo sacan el 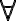$\forall$ sin el negado.

2016 Julio.pdf

Re: Examen Julio 2016 - Ejercicio 1

de Romina Romero - InCo - jueves, 2 de febrero de 2017, 00:43

Hola.

Parte c)

Sí, está bien la justificación. (Recordar que además hay que demostrar que ac sí pertenece a L1).

Parte d)

1) "¿No sería $M \not\models \lnot R(x)$ ? "

No, porque acá ya estamos en el lenguaje de los símbolos. Lo que aparece a la derecha del $\models$ (o $\not\models$ ) (y que está dentro del alcance del $\models$ ) es siempre una fórmula (elemento de FORM), que está en el lenguaje de símbolos. En este caso es una fórmula atómica.

2) Lo que plantea la solución está bien, pero me parece que está complicado un poco de más. En el EVA está la solución subida, y revisada, más sencilla para mi gusto.

"¿No es que si dice ¬ puedo convertirlo y sacarlo en ?" sí, casi, hay que "meter la negación para adentro": $\lnot (\forall x) \varphi(x) \, eq \, (\exists x) \lnot \varphi(x)$

Para entender esto está bueno pensarlo con una oración que tenga sentido: "No todos los días son soleados" es equivalente a "Existen días no soleados".

La solución (la versión más vieja de biblioteca) hace varios pasos juntos, la justificación sería:

$M \not\models (\forall x) \lnot P_1(x)$

$\Leftarrow 2.4.5 \, (\lnot)$

$M \models \lnot (\forall x) \lnot P_1(x)$

$\Leftarrow equivalencia$

$M \models (\exists x) \lnot \lnot P_1(x)$

$\Leftarrow 2.4.5 \, (\exists) \text{ y sust. }$

$(\bar{\exists} u \in C) \, M \models \lnot \lnot P_1(\bar{u})$

$\Leftarrow 2.4.5 \, (\lnot) \text{ (usado en el otro sentido esta vez) }$

$(\bar{\exists} u \in C) \, M \not\models \lnot P_1(\bar{u})$

Como hay una doble negación (no modela la negación de la fórmula) es un poco difícil de ver que en realidad el existe salió "bien" porque metió una negación para adentro antes de irse.

Podríamos verlo, con un ejemplo, como "No es verdad que todos los días son no soleados" es equivalente a "existe un día donde no es verdad que no es soleado", pero es más fácil decir "existe un día soleado".

Cualquier duda volvé a consultar.

Saludos

Romina

Re: Examen Julio 2016 - Ejercicio 1

de Nestor Valentin Etcheverry Olivieri - jueves, 2 de febrero de 2017, 02:41

Perfecto, me queda una dudita:

Entonces cuando se tiene (¿cuando se saca el not del modela es para todo lo que hay a la derecho?)

$M \models \lnot ( (\forall x) \lnot P_1(x) )$

se hace una especie de distributive con ese ¬, un paso intermedio seria

$M \models \lnot (\forall x) \lnot \lnot P_1(x)$

¿y ahi si aplicas el equivalente del $\lnot (\forall x)$ = $(\exists x)$ ?

Re: Examen Julio 2016 - Ejercicio 1

de Romina Romero - InCo - jueves, 2 de febrero de 2017, 23:23

Para poder sacar el not del modela:

hay que tener una sentencia a la derecha (o sea, hay que clausurar primero si hace falta, no puede haber variables libres)
aplica a toda la fórmula a la derecha del modela sí.

No, no es una distributiva del not.

Observar que $\lnot ((\forall x) \varphi)$ es lo mismo que $\lnot (\forall x) \varphi$ , cualquiera sea la fórmula $\varphi$ , ya que en el segundo caso simplemente se están simplificando los paréntesis. $\forall x$ por sí solo no es una fórmula, no es nada, recién cobra sentido cuando tiene una fórmula a su derecha, a la cual cuantifica produciendo una nueva fórmula.

Las fórmulas siempre son como oraciones terminadas, con sentido. Por ejemplo $P(x)$ puede significar, en alguna estructura, "x es lindo/a" (o sea, P se corresponde con la relación "ser lindo/a").

$\forall x$ siempre significa "Para todo"/"Todo". Si alguien viene y dice "Para todo.", uno se queda esperando algo más "¿para todo qué?" "¿qué pasa con el 'para todo'?".

Justamente lo que estamos esperando es esa otra fórmula, "toda ciudad de Uruguay es linda" es una oración completa, que se formó a partir de la oración más simple "es linda" y se cuantificó. Por otro lado "toda ciudad de Uruguay" no está completa (ni siquiera es oración, no tiene verbo). ¿Se entiende?

Prestar atención a que la equivalencia no es "

$\lnot (\forall x) \equiv (\exists x)$ " sino "

$\lnot (\forall x) \equiv (\exists x) \lnot$ ", "no todos" es "hay alguno que no". ¿Queda claro eso? Es importante.

Cualquier duda volvé a consultar, no hay problema.

Saludos