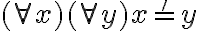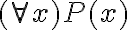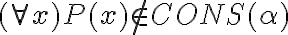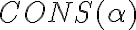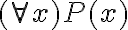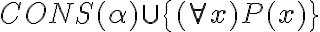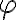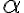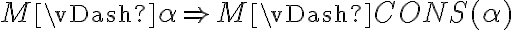[Examen Julio 2015][Ejercicio 4]

[Examen Julio 2015][Ejercicio 4]

de Matteo Guerrieri Garcia -
Número de respuestas: 2

Mi pregunta es sobre el ej 4, parte d.

Tengo un lenguaje del tipo <1;-;0> Con símbolo P.

A su vez tengo una fórmula alfa= (All x)(All y) x='y

Tengo 2 preguntas respecto a esto: 

1- En la sol. dice que (All x)(All y) x='y no pertenece al cons(alfa), porque es eso cierto?

2- Para probar esto, alcanza con encontrar una fórmula, "psi" del cons(alfa) y otra fórmula "phi" tal que haya una estructura que modele {psi} u {phi} ?

Gracias 

En respuesta a Matteo Guerrieri Garcia

Re: [Examen Julio 2015][Ejercicio 4]

de Romina Romero - InCo -

Hola.

1 - Está mal la solución. Una fórmula siempre pertenece a su CONS. Donde dice (\forall x)(\forall y) x =' y debería decir (\forall x)P(x) :

(\forall x) P(x) \not\in CONS(\alpha) . Hay modelos de CONS(\alpha) que no lo son de (\forall x) P(x) .

CONS(\alpha) \cup \{ (\forall x) P(x) \} tiene modelo, es consistente.

Por lo tanto si a CONS(\alpha) le agregamos la fórmula (\forall x)P(x) el conjunto es consistente, o sea CONS(\alpha) no es consistente maximal.


2 - No. Alcanza con encontrar una fórmula  \varphi que no esté en el CONS(\alpha) y mostrar que hay una estructura que modela a la vez a esa \varphi y a todo el CONS. No es suficiente mostrar que la estructura modela a \varphi y a una sola arbitraria del CONS.

Lo que sí alcanza, siendo que es el CONS de una sola fórmula (y no de un conjunto con más de una fórmula), es mostrar que la estructura modela a \varphi y a \alpha , porque si M \vDash \alpha \Rightarrow M \vDash CONS(\alpha) .


Gracias por notar el error y disculpá la confusión. Ya subí una versión corregida del pdf.


Saludos