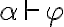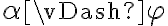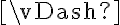Exámenes

Hola.

Pregunta 1: es más general sí. Por definición de estructura, el universo no puede ser vacío (entonces su cardinalidad es ≥ 1). Entonces o bien tiene exactamente un elemento, o bien tiene más de un elemento (por tercero excluido, no hay otra opción). Se cumple para cualquier tipo de similaridad.

Dado un ejercicio con un tipo de similaridad, lo único que interesa son las estructuras de ese tipo, supongo que por eso es el "se consideran todos los modelos del tipo de similaridad dado".

Pregunta 2:

$\varphi \in CONS(\{ \alpha \})$

sii [def CONS]

$\alpha \vdash \varphi$

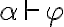
sii [corrección y completitud]

$\alpha \vDash \varphi$

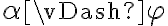
sii [def de 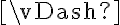$\vDash$ (conjunto de fórmulas modela a fórmula)]

$(\bar{\forall} M \, eta ) (M \vDash \alpha \Rightarrow M \vDash \varphi)$ (eta = estructura de tipo adecuado)

sii

todos los modelos de alfa son modelos de phi

Si el último sii no es claro, fijate que

$(\bar{\forall} M \, eta ) (M \vDash \alpha \Rightarrow M \vDash \varphi)$

se puede reescribir así [usando relativización (ver en las diap de semántica) y la def de Mod]

$(\bar{\forall} M \in Mod(\{ \alpha \}) ) M \vDash \varphi$

y esto es exactamente lo mismo que decimos con lenguaje natural en "todos los modelos de alfa son modelos de phi".

Cualquier duda, consultá.

Saludos