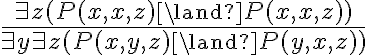Lógica: [Examen Diciembre 2015][Ejercicio 4]

Hola, tengo una duda respecto a la solución propuesta para la parte a. del ejercicio 4 el examen de diciembre de 2015. Concretamente es en esta parte de la solución:

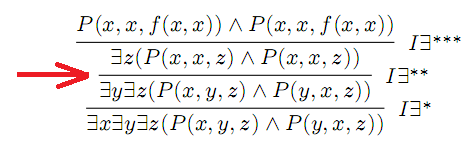
Y la duda es sobre cómo funciona la sustitución (de x por y en este caso) que permitió el pasaje marcado con la flecha. Busqué en el libro y encontré otro ejemplo en donde pasa lo mismo (páginas 92 y 93):

Y explica que el resultado no sería derivable si sólo pudieramos hacer sustituciones para todas las ocurrencias al mismo tiempo. Entonces, esta función de sustitución que se usa en las reglas de eliminación del 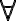$\forall$ e introducción del 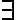$\exists$ , ¿me deja elegir en qué ocurrencias de la variable la aplico, en lugar de aplicarse sobre todas las de la fórmula en cuestión?

Re: [Examen Diciembre 2015][Ejercicio 4]

de Luis Sierra - lunes, 25 de julio de 2016, 16:49

tres comentarios... los primeros dos son los importantes si estás apurado.

1. no te confundas: las reglas usan la función de sustitución usual. es decir, cuando dice phi[t/x] refiere a la fórmula que se obtiene tomando TODAS las ocurrencias libres de x, y cambiándolas por t.

2. el texto de van dalen es confuso en esas líneas. así que, una vez más, no te confundas.

3. comenté esto con otro docente, y la única explicación que se nos ocurre para entender lo que pasa en el texto es el uso de la notación (infeliz) phi(t) en lugar de phi[t/x]. hay cuatro momentos que pueden verse al respecto.

3.1. en pág.63 explica la notación phi(t). una forma que me conviene de explicarla es la siguiente: puedes escribir phi y phi[t/x] (como lo considero adecuado), o seguir una tradición más vieja y escribir phi(x) y phi(t).

3.2. en pág.86 presenta la eliminación de la cuantificación universal, diciendo: si tienes (Ax)phi(x), puedes obtener phi(t). observemos que eso se traduce sin problemas en nuestra notación usada en el curso (y que recomiendo fuertemente): si tienes (Ax) phi, puedes obtener phi[t/x].

3.3. en pág.91, lema 3.9.1.i es el lugar en el que creo se origina la confusión. el lema afirma que si tienes phi(t), puedes obtener (Ex) phi(x). y quizá es ahí en que uno puede creer que la fórmula importante es phi(t) (a fin de cuentas, aparece primero). pero lo que dice el lema es que si tienes una fórmula phi, y una prueba de phi[t/x], puedes obtener (Ex) phi.

3.4. ahora, en el fragmento que citas, termina esta confusa historia. al aplicar la regla de intro del existe parece decir que phi(t) es t='t, y por lo tanto phi(y) debería ser y='y, y comenta (en forma desafortunada) que ese phi(y) debería permitir más que "only make substitutions for all occurrences at the same time". sin embargo, por lo que señalaba en 3.3, lo que sucede es que phi[t/y] es t='t, mientras que phi es t='y.

espero no haberte confundido mucho. este tipo de confusión aparece por el uso desafortunado de la notación phi(t).

saludos

luis

Re: [Examen Diciembre 2015][Ejercicio 4]

de Bruno Enzo Hernandez Biasco - lunes, 25 de julio de 2016, 20:11

Buenas tardes profesor, muchas gracias por responder y por haberse tomado el tiempo de discutir el asunto con otro docente para elaborar su respuesta.

Lo que me pasó con el ejercicio por el que pregunté fue que empecé la demostración ("de arriba hacia abajo") desglosando la hipótesis que incluye cuantificadores universales, entonces como en la regla de eliminación de ese cuantificador se aplica la sustitución luego de eliminarlo, al seguir haciendo el ejercicio me quedé con esa idea. Entonces al ver que decía $\frac{\exists z (P(x,x,z) \land P(x,x,z))}{\exists y \exists z (P(x,y,z) \land P(y,x,z))}$ me surgió la duda, pero en realidad era que estaba leyendo mal la aplicación de la sustitución (en el existencial la sustitución se tiene antes de introducirlo), ahora ya claramente veo que la sustitución de x por y se hizo sobre todas las ocurrencias libres de y.

A pesar de que me di cuenta de eso mientras escribía la pregunta, al final decidí enviarla para ver a qué se debía eso que cité del libro, así que nuevamente le agradezco por haberse tomado el trabajo de habérmelo explicado.

Saludos,

Bruno Hernández.-