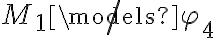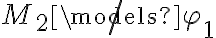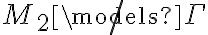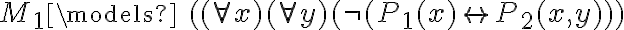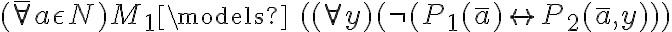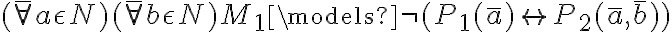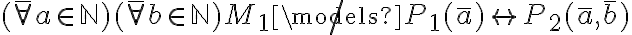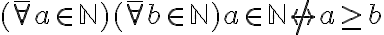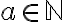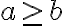Segundo parcial 2016 Ejer 2-c

Segundo parcial 2016 Ejer 2-c

de Alexis Alfonso -
Número de respuestas: 3


No logré llegar a probar esto. Si bien creo que estaba rumbeado porque usé primero el contrarecíproco de Correción con la intención de probar que phi4 no es consecuencia lógica de Γ

Pero, no logré encontrar un modelo de gamma que no sea modelo de phi4. Pensé que podían ser M1 o M2 porque antes

había demostrador que ambos son modelos de gamma, pero llegué a que ambos también modelaban phi4. 

Era más sencillo que esto que pensé?


Gracias

En respuesta a Alexis Alfonso

Re: Segundo parcial 2016 Ejer 2-c

de Romina Romero - InCo -

Hola.

Sí, estabas bien rumbeado. Pero M_1 \not\models \varphi_4 y sí modela a Γ, por lo que servía de testigo.

Por otra parte, M_2 \not\models \varphi_1 por lo cual M_2 \not\models \Gamma .

Si querés intentá hacerlo de vuelta y tal vez encuentres el error, o si no, podés mostrar el desarrollo acá así lo buscamos.


Saludos
En respuesta a Romina Romero - InCo

Re: Segundo parcial 2016 Ejer 2-c

de Alexis Alfonso -

Si, ahora más tranquilo llegué a todo eso que dijiste. O casi en realidad. Porque para probar que  M_1 \not\models \varphi_4

intenté probar lo contrario hasta llegar a una contradicción:

  M_1 \models \ ( ( \forall x )( \forall y )(\neg(P_1(x) \leftrightarrow P_2(x,y)))  

sii 2.4.5

( \bar{\forall} a \epsilon N ) M_1 \models \ (( \forall y )(\neg(P_1(\bar{a}) \leftrightarrow P_2(\bar{a},y)))

sii 2.4.5

( \bar{\forall} a \epsilon N )( \bar{\forall} b \epsilon N ) M_1 \models \neg(P_1(\bar{a}) \leftrightarrow P_2(\bar{a},\bar{b}))

sii 2.4.5

( \bar{\forall} a \epsilon N )( \bar{\forall} b \epsilon N ) M_1 \not\models P_1(\bar{a}) \leftrightarrow P_2(\bar{a},\bar{b})


Y en ese punto alcanzaría con decir, lo cual no se cumple eligiendo como testigos: a = 2 y b = 1  ? Porque no se me ocurre como seguir desarrollando...
En respuesta a Alexis Alfonso

Re: Segundo parcial 2016 Ejer 2-c

de Romina Romero - InCo -

Sí, ese contrajemplo es lo que se precisa para concluir.

Yo agregaría un paso más antes:

( \bar{\forall} a \in \mathbb{N} )( \bar{\forall} b \in \mathbb{N} ) M_1 \not\models P_1(\bar{a}) \leftrightarrow P_2(\bar{a},\bar{b})

sii def modelar fórmula

( \bar{\forall} a \in \mathbb{N} )( \bar{\forall} b \in \mathbb{N} ) a \in \mathbb{N} \not\leftrightarrow a \geq b

y esto es falso, porque tomando a = 2 y b= 1 se cumple que a \in \mathbb{N} y a \geq b (se cumple el sii).


Saludos