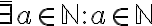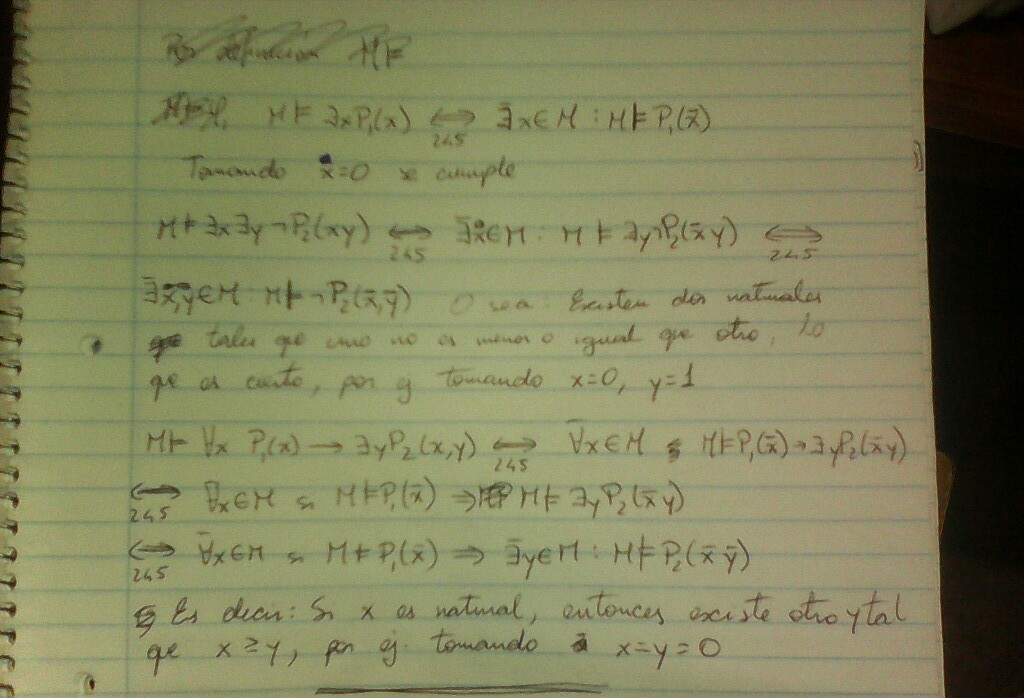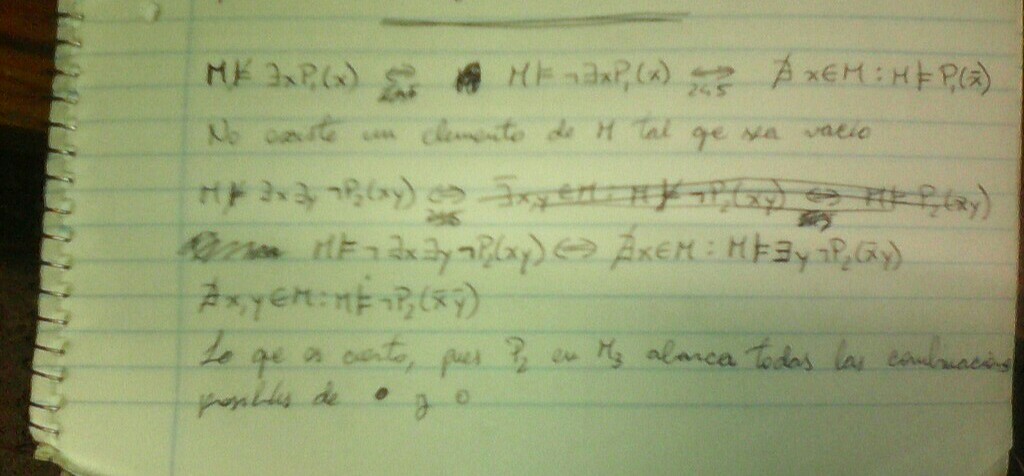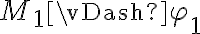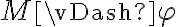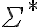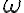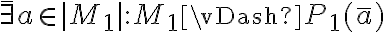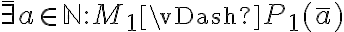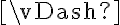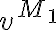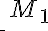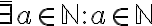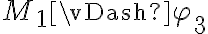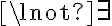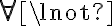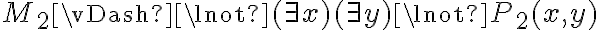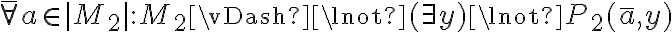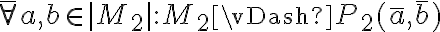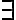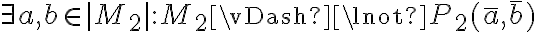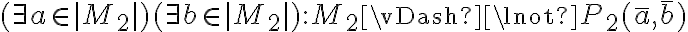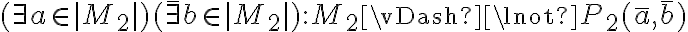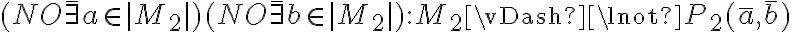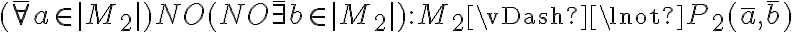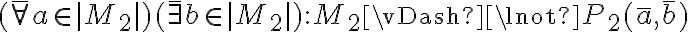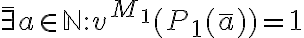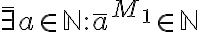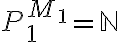Hola.
Observaciones:
Tenés que usar los nombres de las estructuras a las que realmente te estás refiriendo, es decir, si se llama M1, hay que poner 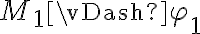 y no
y no 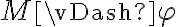 (lo mismo con M2).
(lo mismo con M2).
Cuando usamos el 2.4.5 y sacamos un cuantificador para afuera, el nombre de la variable tiene que cambiar, porque ya no es la "x" que es una variable del lenguaje de primer orden (LPO), sino que es un elemento de nuestro universo, y por tanto no se puede llamar igual, porque son cosas distintas y porque sino no queda clara esa distinción. Por convención, usamos las últimas letras del alfabeto (w,x,y.z) para las variables del LPO y las primeras (a,b,c) para los elementos del universo (no es estricta, capaz que si el universo es 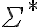 resulta más natural usar
resulta más natural usar 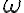 en vez de a).
en vez de a).
Además, los elementos pertenecen al universo de la estructura, lo que se representa poniendo barras a los lados de la estructura: |M1| (o usando el nombre del universo, si es que tiene).
Entonces sería, por ejemplo, 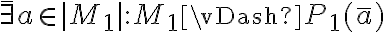 o también
o también 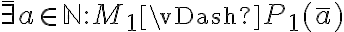 .
.
Antes de poder justificar que una sentencia se cumple (o no) para una estructura dada, hay que terminar la "traducción" desde el LPO al metalenguaje, debemos interpretar las fórmulas y los términos, hacer desaparecer el "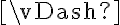 " y la
" y la 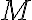 .
.
Por ejemplo, en la primera parte falta este paso:
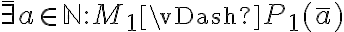
sii [def 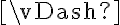 ,
, 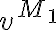 y
y 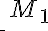 (def modelar fórmulas, interpretación de fórmulas e interpretación de términos)] *
(def modelar fórmulas, interpretación de fórmulas e interpretación de términos)] *
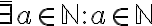
Ahora sí tenemos algo completamente expresado en metalenguaje, y podemos decir "tomando x = 0 se cumple".
La justificación de 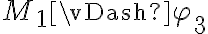 está mal, porque tenemos que probar un para todo, por lo que no alcanza mostrar que funciona para un ejemplo (x = y = 0). Hay que mostrar que para cualquier x va a existir un y que sea mayor o igual (podríamos decir que alcanza con tomar y = x, pero sin igualar a 0).
está mal, porque tenemos que probar un para todo, por lo que no alcanza mostrar que funciona para un ejemplo (x = y = 0). Hay que mostrar que para cualquier x va a existir un y que sea mayor o igual (podríamos decir que alcanza con tomar y = x, pero sin igualar a 0).
En la parte de  , no es que el elemento sea vacío, sino que pertenezca al conjunto vacío.
, no es que el elemento sea vacío, sino que pertenezca al conjunto vacío.
Los 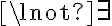 es mejor sacarlos como
es mejor sacarlos como 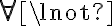 :
:
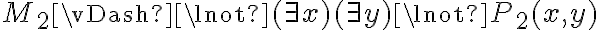 sii
sii 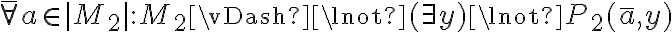 sii
sii  sii
sii 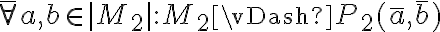 .
.
Si los sacás como 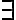 , que es más bien un abuso de notación, no tiene que quedar:
, que es más bien un abuso de notación, no tiene que quedar:
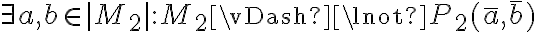 , que es una abreviación de
, que es una abreviación de 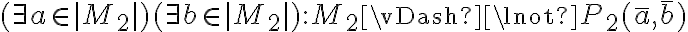
sino
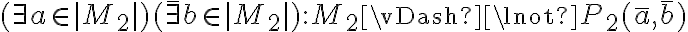 .
.
Porque:
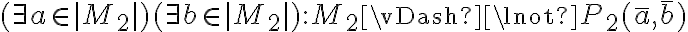
sii [notación]
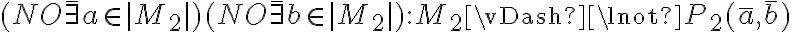
sii [equivalencia]
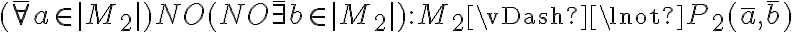
sii [equivalencia]
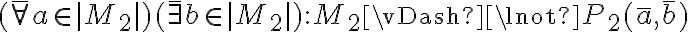
Manejar  es mucho más confuso y propenso a errores.
es mucho más confuso y propenso a errores.
Lo demás se ve bien.
Saludos
* En realidad son varios pasos comprimidos, que se pueden comprimir siempre que en la justificación se incluya todo lo que se está haciendo):
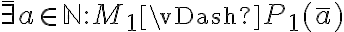
sii [def 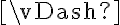 ]
]
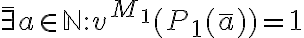
sii [def 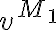 ]
]
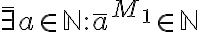 (obs.:
(obs.: 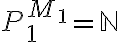 )
)
sii [def interpretación términos]