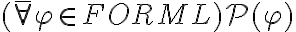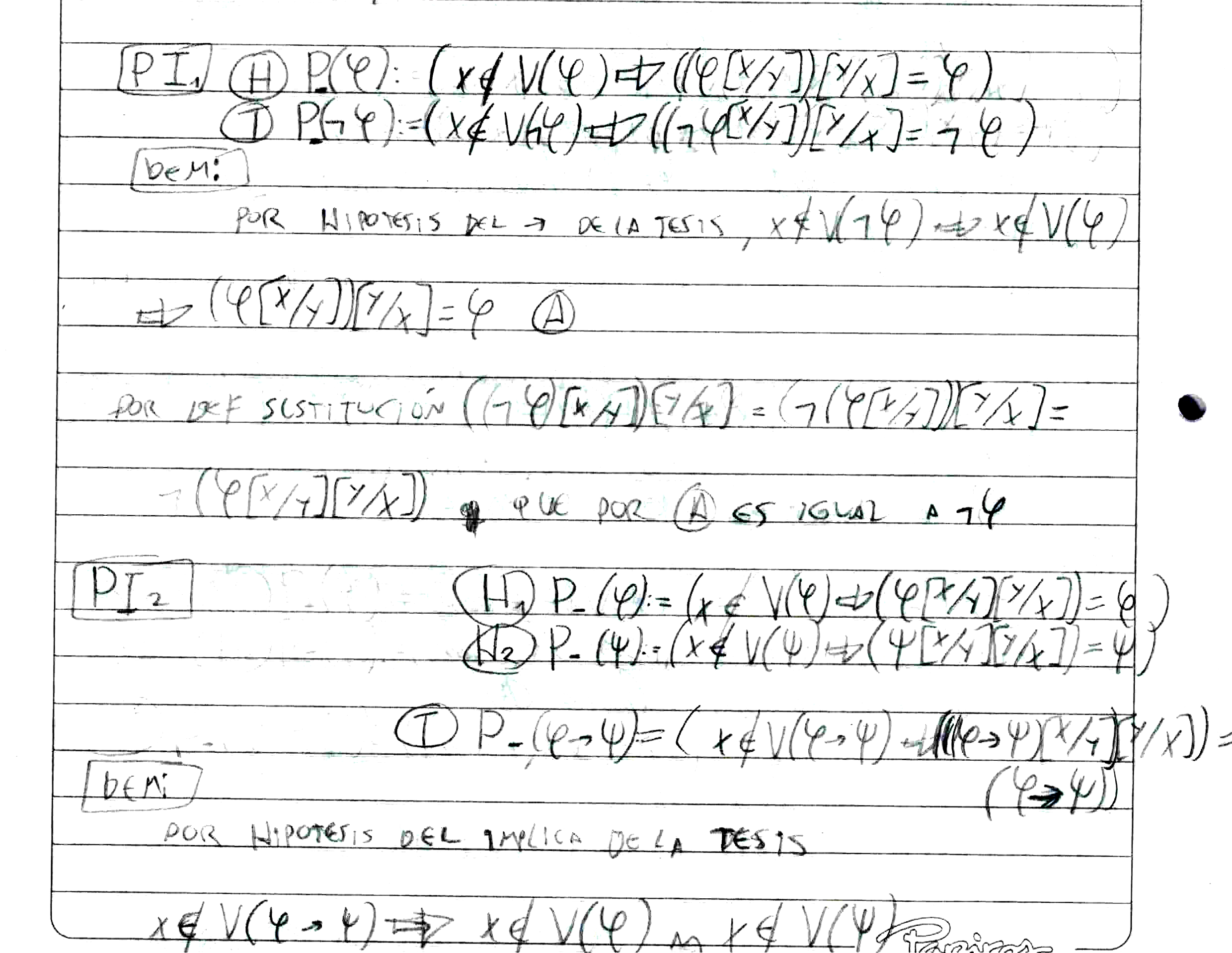Hola.
En el enunciado del PIP te falta la tesis (penúltima línea del algoritmo que escribí antes). Solo escribiste las hipótesis.
"Hice el lema pero nose si alcanza esa justificación para las
variables xi, que como no hay cuantificadores siempre se puede realizar
la justificación" El lema está bien. En la sustitución en TERM no hay restricciones, siempre se puede sustituir. La restricción de que el término tiene que estar libre para variable en la fórmula, es solo para sustituciones en FORM.
"Tendría que haber puesto primero el lema, PIP del lema, la parte de FORM, PIP en FORM pero me quedo en ese orden" el lema puede estar después de la demostración por inducción en FORM, eso no es problema. Además es más natural que te des cuenta que precisás el lema una vez que estás metido en la demostración. Lo que sí, yo pondría la conclusión de FORM "como P cumple con el PIP de FORM...." justo después del último paso inductivo en FORM. Y luego el lema. Supongo que a eso te referías con
"si me olvide del final del PIP".
La demostración en general se ve bien.
Saludos




![(\bar{\forall} \varphi \in FORM_\mathcal{L})(\bar{\forall} x,y \in VAR)(x \not\in V(\varphi) \Rightarrow (\varphi[x/y])[y/x] = \varphi ) (\bar{\forall} \varphi \in FORM_\mathcal{L})(\bar{\forall} x,y \in VAR)(x \not\in V(\varphi) \Rightarrow (\varphi[x/y])[y/x] = \varphi )](https://eva.fing.edu.uy/filter/tex/pix.php/af07e5e2974ac47925224076ea142428.gif)
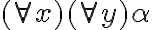
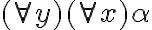
![(\bar{\forall} x,y \in VAR)(\bar{\forall} \varphi \in FORM_\mathcal{L})(x \not\in V(\varphi) \Rightarrow (\varphi[x/y])[y/x] = \varphi ) (\bar{\forall} x,y \in VAR)(\bar{\forall} \varphi \in FORM_\mathcal{L})(x \not\in V(\varphi) \Rightarrow (\varphi[x/y])[y/x] = \varphi )](https://eva.fing.edu.uy/filter/tex/pix.php/5b4116bc96dfe6914c41ad897a15fdfe.gif)
![(\bar{\forall} \varphi \in FORM_\mathcal{L})(x \not\in V(\varphi) \Rightarrow (\varphi[x/y])[y/x] = \varphi ) (\bar{\forall} \varphi \in FORM_\mathcal{L})(x \not\in V(\varphi) \Rightarrow (\varphi[x/y])[y/x] = \varphi )](https://eva.fing.edu.uy/filter/tex/pix.php/29f5db60a0ccab5e334d7437fc8dffe2.gif)
![\mathcal{P}(\varphi) := x \not\in V(\varphi) \Rightarrow (\varphi[x/y])[y/x] = \varphi \mathcal{P}(\varphi) := x \not\in V(\varphi) \Rightarrow (\varphi[x/y])[y/x] = \varphi](https://eva.fing.edu.uy/filter/tex/pix.php/4fba8212a2896fa444cd0dc40f2081a0.gif)
![(\bar{\forall} t \in TERM)(x \not\in V(t) \Rightarrow t[x/y][y/x] = t ) (\bar{\forall} t \in TERM)(x \not\in V(t) \Rightarrow t[x/y][y/x] = t )](https://eva.fing.edu.uy/filter/tex/pix.php/87bf7a59183237a4304211a5fd6c3e10.gif)
![((\forall y)\varphi)[x/y][y/x] = (((\forall y)\varphi)[x/y])[y/x] = ((\forall y)\varphi)[y/x] ((\forall y)\varphi)[x/y][y/x] = (((\forall y)\varphi)[x/y])[y/x] = ((\forall y)\varphi)[y/x]](https://eva.fing.edu.uy/filter/tex/pix.php/5e2dd1e903b50b37b2096503e1dc351f.gif)
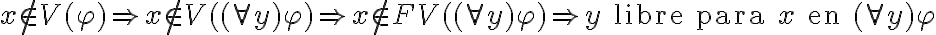
![((\forall y)\varphi)[y/x] = ((\forall y)\varphi[y/x]) = (\forall y)\varphi ((\forall y)\varphi)[y/x] = ((\forall y)\varphi[y/x]) = (\forall y)\varphi](https://eva.fing.edu.uy/filter/tex/pix.php/85baa6221b4087d0c2285a3ad448ba83.gif)