Lógica: Segundo Parcial 2014, Ej 2) b) II) 1)

Tengo 2 existe X, uno a cada lado del tenedor de 2 patas, ¿Puedo tomarlos por separado? Osea poner de un lado existe X y del otro existe Y.

Ademas, que eso se cumpla o no, ¿No depende de la estructura con la que se esté trabajando?

Re: Segundo Parcial 2014, Ej 2) b) II) 1)

de Romina Romero - InCo - domingo, 26 de junio de 2016, 20:26

Hola.

Ya están "por separado", porque cuando una variable está alcanzada por un cuantificador, funciona como una variable local (como en programación) a ese cuantificador.

Por ejemplo, en la fórmula 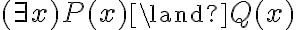$(\exists x) P(x) \land Q(x)$ , el alcance del cuantificador es P(x), y por tanto la x de la P no tiene por qué ser la misma que la x de la Q (la x de la P es una variable local al cuantificador, la de la Q es global).

Si fuera 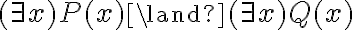$(\exists x) P(x) \land (\exists x) Q(x)$ , serían dos variables locales distintas, totalmente separadas.

Si querés cambiar las variables, el teorema 2.5.4 te explica de cuándo y cómo se pueden cambiar. Y en caso de hacer un cambio de variable, hay que justificar que se cumple con este teorema.

Respecto a tu segunda pregunta, la respuesta no depende de la estructura con la que se esté trabajando. El símbolo 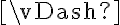$\vDash$ está sobrecargado, si se quiere. Para saber qué significa, tenemos que ver de qué tipo son las cosas que tenemos a la izquierda y derecha del símbolo.

En este caso: $(\exists x) t_0 =' x \vDash (\exists x) t_{k+1} =' x$

a la izquierda tenemos un conjunto de fórmulas (de hecho, es una fórmula, pero porque, por convención, se omiten las llaves de conjunto), y a la derecha tenemos una fórmula. O sea, estamos ante algo de la forma 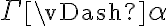$\Gamma \vDash \alpha$ . La def 2.4.4 nos dice que:

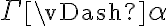$\Gamma \vDash \alpha$ sii [para toda estructura M del tipo adecuado, si M |= φ para todo φ ∈ Γ , entonces M |= α]

¿Se entiende?

Saludos

Re: Segundo Parcial 2014, Ej 2) b) II) 1)

de Nestor Valentin Etcheverry Olivieri - sábado, 2 de julio de 2016, 17:37

Si, eso lo entiendo, entonces si llego a que para toda estructura M, M modela (Ex)t0 = x, M va a modelar (Ex) tk+1 = x y ahí termina el ejercicio? Osea, ¿Solo hay que trabajar con la parte izquierda del tenedor? ¿En la parte derecha puede haber cualquier cosa y no cambia el ejercicio?

Re: Segundo Parcial 2014, Ej 2) b) II) 1)

de Romina Romero - InCo - domingo, 3 de julio de 2016, 20:37

Creo que ahora entendí mejor por qué venía tu duda de hacer el cambio de variable.

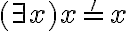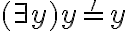Si quisieras cambiar la variable, podrías, pero primero tenés que remplazar t₀ por lo que realmente significa, entonces pasarías de $(\exists x) x =' x$ a $(\exists y) y =' y$ (o con la variable que eligieras). Lo mismo con t_k+1, si la variable del cuantificador cambiara, la de adentro del término también.

"¿En la parte derecha puede haber cualquier cosa y no cambia el ejercicio?" no, cambia sí.

$\Gamma \models \varphi$ sii [def $\models$ ] $(\bar{\forall} M \text{ eta} ) ( M \models \Gamma \Rightarrow M \models \varphi )$ .

El único caso en que no importa la parte derecha, es cuando la parte izquierda es falsa en todas las estructuras. Pero no es el caso de este ejercicio.

Si la frase fuera verdadera, habría que probar:

para toda estructura M, $(\bar{\forall} k \in \mathbb{N}) ( M \models (\exists x)t_0 =' x \Rightarrow M \models (\exists x) t_{k+1} =' x)$

Sustituyendo t₀ por lo que realmente significa:

para toda estructura M, $(\bar{\forall} k \in \mathbb{N}) ( M \models (\exists x) x =' x \Rightarrow M \models (\exists x) t_{k+1} =' x )$

Como el antecedente es verdadero en todas las estructuras (hay que probarlo, pero es fácil ver que es verdadero), la implicancia va a ser verdadera sii el consecuente siempre es verdadero. Pero no siempre lo es. La frase es falsa.

Hay que buscar un contraejemplo, esto es, mostrar que se cumple que

existe estructura M, $(\bar{\exists} k \in \mathbb{N}) ( M \models (\exists x) x =' x \text{ y } M \not\models (\exists x) t_{k+1} =' x )$ .

Hay que elegir un M y un k que no modelen el consecuente.

Recomiendo elegir k = 0 y M = M2, el de la parte bI. Probar:

$\mathcal{M}_2 \models (\exists x) x =' x \text{ y } \mathcal{M}_2 \not\models (\exists x) t_1 =' x$

(observar que parte de la justificación ya está hecha en el ejercicio bI, no hace falta repetirla).

Saludos