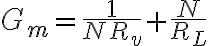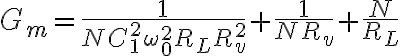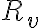Hola, estaba repasando este tema en mi cuaderno de teórico (2014), y en aquella ocasión se dio sin demostración una expresión medio larga para la transferencia 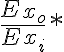 . De allí surgía una fórmula para la frecuencia de oscilación,
. De allí surgía una fórmula para la frecuencia de oscilación,
Después se explicó que en el caso 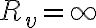 se reduce a
se reduce a
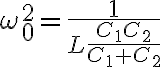
Mi duda surge porque las unidades de los dos términos del denominador son incongruentes: el primero 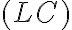 tiene unidades de
tiene unidades de 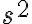 y el segundo
y el segundo 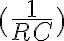 de
de 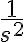 .
.
Haciendo ![IM[\frac{E_{x_o}}{E_{x_i}}] = 0 IM[\frac{E_{x_o}}{E_{x_i}}] = 0](https://eva.fing.edu.uy/filter/tex/pix.php/1eb210d63211bff1fd8715bf37de429d.gif) yo obtuve
yo obtuve
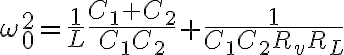
Entiendo que esto no aporta mucho, porque en general se trabaja con la aproximación, pero quisiera que me aclararan si están bien la transferencia y el valor de 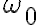 que hallé.
que hallé.
Muchas gracias.

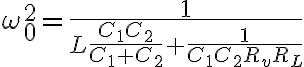
![*\frac{E_{x_o}}{E_{x_i}} = \frac{G_mR_L L s R_v C_1 s}{R_L Ls(R_vC_2s + 1)C_1s + (R_L + Ls)[R_v(C_1 + C_2)s + 1]} *\frac{E_{x_o}}{E_{x_i}} = \frac{G_mR_L L s R_v C_1 s}{R_L Ls(R_vC_2s + 1)C_1s + (R_L + Ls)[R_v(C_1 + C_2)s + 1]}](https://eva.fing.edu.uy/filter/tex/pix.php/c1c024c6edc3e1df8517f8418d60bcc7.gif)