S dx / x*sqrt(4+x^2)
Hola, me gustaría que me dijeran como se resuelve esta integral, le di mil vueltas y no me sale. Gracias.
En respuesta a Fabian Nicolas Troche Gutierrez
Re: Ej 11 (6) Practico 8
Te lo escribí lo más claro posible paso a paso. Cualquier duda a las ordenes ;)
P/D: ARCTH es arco tangente hiperbólico. Se me escapó la g. :/
En respuesta a Ezequiel Eduardo Dutra Ordeix
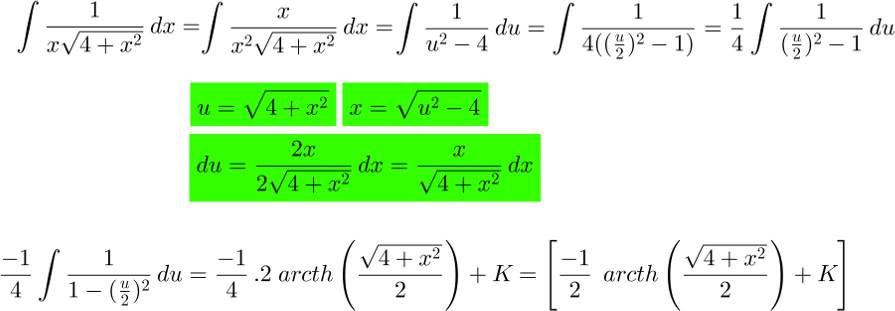
Re: Ej 11 (6) Practico 8
Una pregunta, como aparece el 2 que multiplica a arcotangente hiperbolico en el último renglón?
Llegue hasta ahí pero no entendí de donde sale. Gracias.
En respuesta a Ignacio Rafael Ferreira Urrutia
Re: Ej 11 (6) Practico 8
Es por la regla de la cadena (derivadas) siempre que derivás el arcotangente hiperbólico (de igual forma para otras funciones compuesta) te queda algo como en el primer reglón de la figura.
Ahora, cuando derivás el arcotangente hiperbólico del ejercicio te queda multiplicado por 1/2 (porque 1/2 es el coeficiente de u), para corregir esto, multiplicás el arcotangente hiperbólico por la inversa de 1/2 (en este caso 2). Así te queda el valor al que llegaste y no otro.
Si fuera u/3 deberías multiplicar por 3. Así en TODOS los casos de estas características. ;)
P/D: Si querés verlo de otra forma, es como decir; lo que tengo acá se parece a la derivada del arcotangente hiperbólico pero multiplicada por 2.
En respuesta a Ezequiel Eduardo Dutra Ordeix
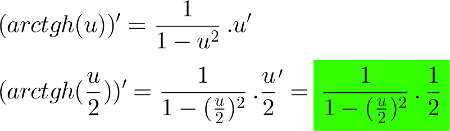
Re: Ej 11 (6) Practico 8
Entonces la primitiva cuando la derivas si no le agregas el dos, por la regla de la cadena te agrega el 1/2 que no es la integral buscada, ahora si. Voy a empezar a derivar las primitivas que encuentre en caso de duda para darme cuenta en esos casos.
Genial che, gracias por armar toda la explicación y tomarte el tiempo de contestar.Saludos
En respuesta a Ignacio Rafael Ferreira Urrutia
Re: Ej 11 (6) Practico 8
Dale, a las ordenes y mucha suerte! ;)
Si bien la resolución planteada es correcta, otra posible forma de integrar $$\frac{1}{u^2-4}$$ es utilizar fracciones simples (esta es la forma que se vió en el curso):
$$\int \frac{1}{u^2-4}\,du =\frac{1}{4}\left(\int \frac{1}{u-2}\,du - \int \frac{1}{u+2}\,du \right)$$
$$\int \frac{1}{u^2-4}\,du=\frac{1}{4}\left[\text{log}(u-2)-\text{log}(u+2)\right]+k$$
Les dejo como ejercicio utilizar la definición de arcotangente hiperbólico para verificar que está solución es equivalente a la que plantearon más arriba.
Saludos
Muchas gracias a los dos, quedo todo claro, saludos.