Parciales

Sí, la idea está bien.

Yo tendría un poco más de cuidado al expresar esta parte: "el valor del resto de los p(i+1) ↔ -p(i) queda determinado por los valores inciales de p1 y p0"

En realidad, el valor de p(i+1) ↔ -p(i) queda determinado por los valores de p(i) y p(i+1). Los valores de estas letras están determinados por la valuación que estemos considerando. Como queremos considerar las valuaciones que satisfacen a 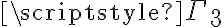$\scriptstyle{\Gamma_3}$ y p(i+1) ↔ -p(i) son fórmulas de ese conjunto, queremos las valuaciones que hagan 1 a esas todas esas fórmulas y a 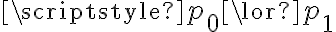$\scriptstyle{p_0 \lor p_1}$. Por tanto, para satisfacer al conjunto, los valores que nos sirven para p2, p3, .... dependen de los valores que tomemos para p0 y p1.

Podríamos decir entonces: "para satisfacer al resto de las fórmulas, el valor del resto de las pi (i > 1) depende del valor que tomemos para p0 y p1: si v(p0) = 0 y v(p1) = 1, entonces ......; si v(p0)=1 y v(p1)=0, entonces....." (explicando en "...." cuál es exactamente el valor que deben tomar las otras pi).

"como las únicas dos valuaciones posibles que tengo siempre me hacen 1 a p0 o a p1 no tendría problema?" exacto, siempre una de las dos partes del or va a valer 1, entonces el or vale 1.

Lo último que dijiste sobre 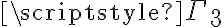$\scriptstyle{\Gamma_3}$ está bien también, convendría explicitar cuál es la valuación (el valor para cada pi).

Sobre 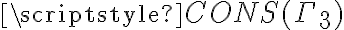$\scriptstyle{CONS(\Gamma_3)}$ lo que podés observar es que 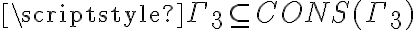$\scriptstyle{\Gamma_3 \subseteq CONS(\Gamma_3)}$ (¿por qué?) y que tenés una única valuación que satisface a 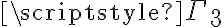$\scriptstyle{\Gamma_3}$. Tendrías que ver si esa valuación también satisface a las otras fórmulas 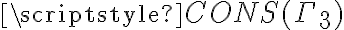$\scriptstyle{CONS(\Gamma_3)}$ o no (teniendo 1 o 0 valuaciones para el CONS, según lo que puedas concluir).

Cualquier duda volvé a consultar.

¡Saludos!