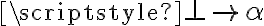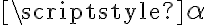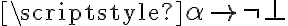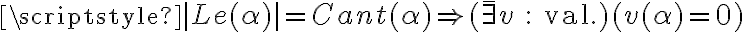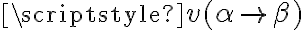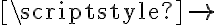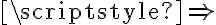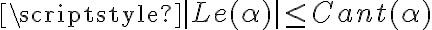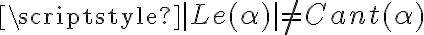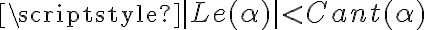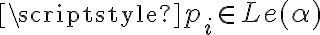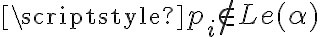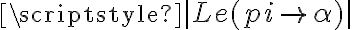Parciales

"Si tengo que probar algo del estilo: si f(a) = g(a) → ocurre Q. Probándolo por inducción, tengo que partir de la base de que f(a) = g(a), verdad?"

No tenés que, podés. Vos tenés que probar que la implicancia es verdadera. Para ello podés partir del antecedente (f(a) = g(a)) y mostrar que se cumple el consecuente (ocurre Q). Pero si el antecedente es falso, como bien decís " la implicancia se cumple". Entonces en ese caso ya está, con mostrar que el antecedente es falso ya está. Asimismo, si el consecuente siempre se cumple, también, con mostrar eso no te importa lo que le pasa al antecedente.

Va a depender cada caso.

Por ejemplo:

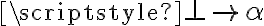$\scriptstyle{\bot \rightarrow \alpha }$ se cumple sin importar el 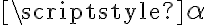$\scriptstyle{\alpha}$ porque el antecedente siempre es falso.

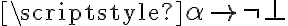$\scriptstyle{\alpha\rightarrow \neg\bot }$ se cumple sin importar el 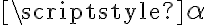$\scriptstyle{\alpha}$ porque el consecuente siempre es verdadero.

¿Se ve?

"En el caso particular del ejercicio 1b del 2011" 1d supongo.

" tengo que Le(alfa) <> Cant(alfa) por lo que al ser falso el antecedente (de mi HI), existe una valuación que me hace falsa a alfa" no.

Calculo que tenés una HI así: 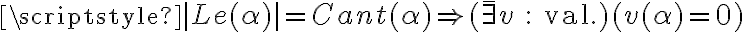$\scriptstyle{| Le(\alpha) | = Cant(\alpha) \Rightarrow (\bar{\exists} v \text{ : val.} )(v(\alpha) = 0)}$. Si tu antecedente no se cumple, no sabés nada del consecuente.

Pensalo así: "si me saco el 5 de oro, me compro una mansión". No me saqué el 5 de oro ¿me compré una mansión? (y capaz que sí con otra plata, capaz que no).

"Puedo considerar que esa valuación además me hace verdadero a pi para que v(pi -> alfa)=0?" No. No podés suponer nada que no se deduzca de las hipótesis que tenés.

Ante estas dudas siempre sirve plantearse un caso simple y ver si lo que estamos diciendo parece tener sentido (no se garantiza que lo que digamos esté bien a partir de un ejemplo, pero si podemos llegar a garantizar que está mal): Si alfa=p0 y pi= p2, existen v1 y v2 valuaciones / v1(p0) = v2(p0) = 0 y v1(p2) = 0 y v2(p2) =1. Como no tenés más datos de con qué valuación estás trabajando, no podés asegurar si estás trabajando con algo como v1 o como v2 (además de que en realidad no podés decir que tenés una valuación que haga 0 a alfa por la parte anterior).

"O directamente como pertenece sucede que Le(pi -> alfa) <> Cant(pi -> alfa) y existe tal valuación?" no, no hay forma de desprender que exista la valuación, pero no importa, porque si no se cumple el antecedente ya está, la implicancia se cumple.

"En el caso que pi no pertenece a Le(alfa), se cumple mi hipótesis inductiva y tengo que existe una valuación v tal que v(alfa)=0. Puedo además decir que esa valuación cumple v(pi)=1?" Sí, pero tenés que justificar por qué. (La idea es que las condiciones que hacen que una valuación cumpla v(alfa) = 0 solo tienen que ver con las letras proposicionales que aparecen en alfa, y pi no aparece)

Acá la duda siempre es la misma, y es ¿cómo funciona un implica? ¿cómo se define el valor de 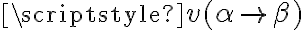$\scriptstyle{v(\alpha \rightarrow \beta)}$? Tanto a nivel de 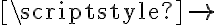$\scriptstyle{ \rightarrow}$ como de 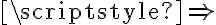$\scriptstyle{ \Rightarrow}$. El funcionamiento siempre es el mismo.

Te recomiendo fuertemente repasar la definición del implica y de valuación en general.

Cualquier cosa volvé a consultar.

Saludos

[EDIT: Corrijo una parte que había dicho mal sobre "el caso que pi no pertenece a Le(alfa)", ya estaba mareada, disculpen]