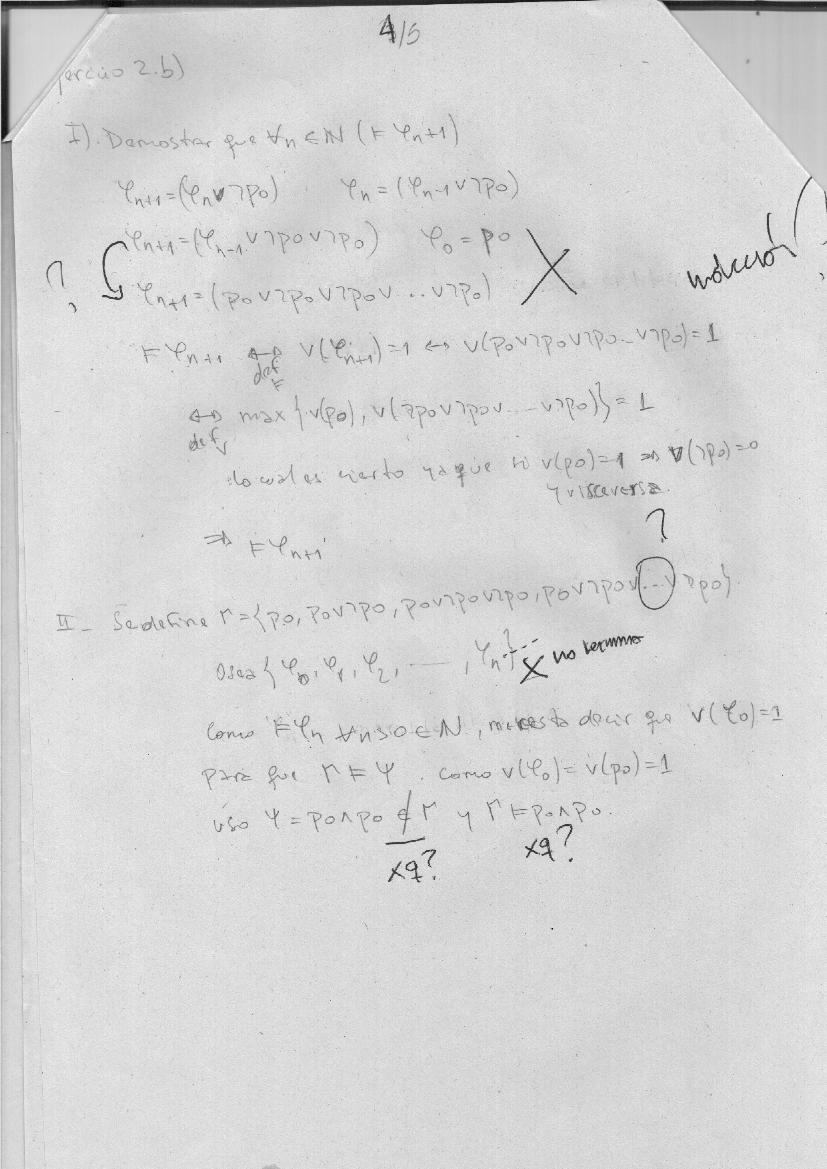Parte a.I. Correcto. Presenta una prueba para justificar la afirmación;
la misma presenta problemas atribuíbles a dificultades en el manejo
de las cuantificaciones.
aI.1. No indica con claridad si la oración es verdadera o falsa. A pesar de
eso, claramente da una prueba, y por lo tanto una respuesta implícita.
aI.2. Escribe "|= phi \/ psi para cierto psi y todo phi". Diría que esa
frase es (Exi psi :: (All phi :: ...)); pero el enunciado
es (All phi :: (Exi psi :: ...)). Me genera dudas acerca de si
decodifica adecuadamente las cuantificaciones en las
oraciones.
aI.3. Usa mal la definición de tautología: dice que
"|= phi \/ psi sii v (phi \/ psi) = 1", pero no dice si v es
cualquier valuación o alguna específica. Debería hablar de
"cualquier valuación". Refuerza mi creencia de que
tiene dificultades para trabajar con cuantificaciones.
Parte a.II. Correcto. Presenta un argumento algo complicado, escrito
con poca claridad.
aII.1. Reaparece el problema de aI.3. En este caso, le genera problemas; afirma
"|=/= phi <-> bottom sii v(phi <-> bottom) = 0", pero en este caso
debe hablar de "alguna valuación". Definitivamente, tiene dificultades
para manejarse con cuantificaciones.
aII.2. Su argumento parece ser el siguiente. Por un lado, argumenta
|=/= phi <-> bottom
<==>
(Exi v :: v.phi = 1)
y por otro,
|= phi -> psi
<==>
(All v :: v.(phi -> psi) = 1)
==> (por el argumento anterior)
(Exi v :: v.psi = 1)
A partir de esto llega a una contradicción, tomando psi = bottom.
aII.3. A pesar de que el argumento es razonable, no está escrito con claridad.
Conspiran contra ello tanto la misma complejidad de su argumento
como la liviandad conque trata las cuantificaciones. La misma situación
señalada en aI.1. atenta para darse cuenta rápidamente que está refutando la
afirmación dada.
Parte b.I. Mal.
bI.1. No formaliza su argumento inductivo. A partir de un manejo preformal
de la inducción concluye que las fórmulas deben ser de la forma
p0 \/ -p0 \/ -p0 \/ ... \/ -p0, sin reflexionar sobre el mecanismo
de formación de las phi.
bI.2. Como consecuencia de bI.1, confunde los paréntesis. Mientras que
phi_2 es (p0 \/ -p0) \/ -p0, considera que es p0 \/ (-p0 \/ -p0)
bI.3. Reaparece el problema de aI.3.
Parte b.II. Mal. Elige un testigo, pero no muestra que lo sea. Además,
ese testigo no aparece vinculado al resto del texto.
bII.1. Considera que Gamma es finito, lo que es claramente contrario al
enunciado. También considera una valuación v que asigna 1 a p0, pero
no queda claro la razón de la misma. Incluso sostiene "me resta decir
que v.p0 = 1"; ¿para qué precisaría realizar esa afirmación? Parecería
creer que tiene que probar la consistencia de Gamma.
bII.2. Elige un psi, y afirma que cumple con dos de los requerimientos
(Gamma |= psi y psi notin Gamma). Sin embargo, no justifica sus afirmaciones
ni plantea el tercer requerimiento (|=/= psi).
.......
En resumen.
Pros: legible; maneja la definición de valuación y la de consecuencia semántica.
Cons: presenta dificultades al presentar sus argumentos; no justifica sus
afirmaciones; no formaliza la inducción, ni visualiza el objeto construído
inductivamente; no es claro si maneja la noción de tautología.