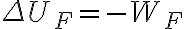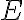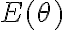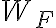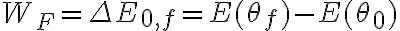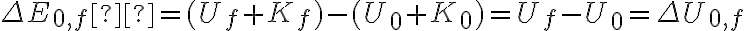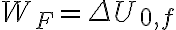F1 - 1S: Práctico 6 Ejercicio 11

Hola, buenas tardes.

Estoy teniendo algun problema para corroborar si mi razonamiento con este ejercicio es correcto. Adjunto a continuación la letra y mi desarrollo:

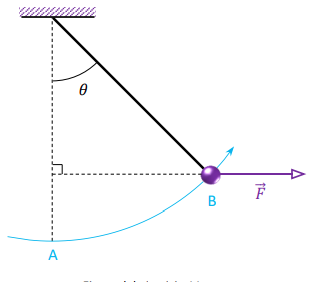
image%20%282%29.png

La primera observación que realicé es que el trabajo realizado por la tensión de la cuerda es cero, por ser perpendicular al movimiento de la esfera.

Luego, creí que sería más comodo trabajar en coordenadas polares 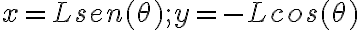$x = Lsen(\theta) ; y = -Lcos(\theta)$ , aunque no se si este paso sea realmente necesario.

Así, partiendo de 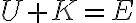$U + K = E$ , sabiendo que la única fuerza conservativa actuante es el peso y que la velocidad 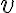$v$ de la esfera se mantiene constante, llegue a la siguiente igualdad: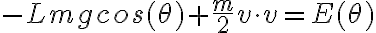 $-Lmgcos(\theta) + \frac{m}{2} v \cdot v = E(\theta)$

Cuando supuse que la única fuerza conservativa actuante era el peso, hice otra suposición implicita y es que la fuerza 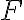$F$ es no conservativa, por lo tanto $E(\theta) = -W_F$ .

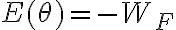Finalmente, para llegar al trabajo efectuado por 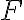$F$ en el arco 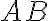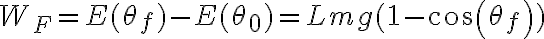$AB$ : $W_F = E(\theta _f) - E(\theta _0) = Lmg(1-cos(\theta _ f))$ , pues $\theta _0 = 0$ .

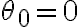¿Es este razonamiento adecuado? Gracias y saludos de antemano.

Re: Práctico 6 Ejercicio 11

de Nicolás Casaballe - jueves, 29 de mayo de 2025, 14:05

Hola, Franco. Tu razonamiento tiene las ideas básicas correctas y además llegaste al resultado buscado. Hay algunos aspectos del planteo que necesitan ser más precisos.

El uso de coordenadas polares es correcto. Tampoco sé si es necesario, pero de todos modos al final hay que establecer una relación entre el desplazamiento del objeto en el espacio y el ángulo, así que las coordenadas polares ya nos adelantan esa tarea.

Está bien suponer que la fuerza F es no conservativa. No hay información para suponer otra cosa. Incluso en el caso de que por alguna razón la fuerza resultase ser al final conservativa, esto no afectaría la solución. Si fuera conservativa, sería posible asociarle una energía potencial. La variación de esta energía potencial sería $\Delta U_F = -W_F$ , y habría que tomarla en cuenta como parte de la energía mecánica $E$ . Sería interesante si puedieras comprobar que esto es efectivamente así.

Lo más importante para corregir está en el balance de energía que propusiste en la primera ecuación entre $E(\theta)$ y $W_F$ . Allí te falta tomar en cuenta la variación de energía mecánica. Tampoco le debemos agregar un signo negativo al trabajo en la ecuación. Es el propio trabajo el que puede ser positivo o negativo.

La expresión correcta debería ser la que pusiste a continuación, que sí está bien:

$W_F = \Delta E_{0,f} = E(\theta_f)-E(\theta_0)$

Cuando expresas la variación de energía mecánica usando las energías potencial y cinética, te queda

$\Delta E_{0,f} = (U_f + K_f) - (U_0 + K_0) = U_f - U_0 = \Delta U_{0,f}$

Esto lo que hace es mostrar que, en este sistema, el cuerpo gana energía potencial gravitatoria gracias al trabajo de la fuerza F, ya que $W_F = \Delta U_{0,f}$ (mientras que su energía cinética no cambia).

Saludos,
NC