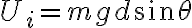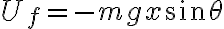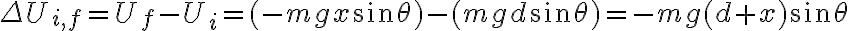Consultas de Física

Hola, Mahicol. Es buena pregunta. La respuesta es a la vez un poco simple y un poco complicada.

Los valores de la energía potencial de una fuerza siempre dependen del punto de referncia elegido. De hecho, el valor de la energía "absoluta" 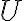$U$ en realidad no tiene un significado físico intrínseco. Lo que sí tiene sentido físico son las variaciones de energía 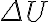$\Delta U$, que corresponden al opuesto del trabajo realizado por la fuerza conservativa en una trayectoria entre dos puntos.

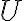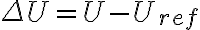Para darle sentido a la energía, debemos considerar el valor de $U$ en un punto dado como el opuesto del trabajo desde el punto de referencia hasta allí. En el punto de referencia la energía es $U_{ref} = 0$, y entonces nos queda $\Delta U = U - U_{ref}$. Pero el valor va a depender de la elección del punto de referencia.

En el ejercicio que estás considerando, por ejemplo, podrías haber tomado como punto de referencia el punto más alto posible de la masa. Si lo haces de esa manera, la energía potencial gravitatoria te queda negativa en todas las partes de la rampa. No hay ninguna contradicción en hacerlo de esta manera.

En tu planteo, el punto de referencia está en el sitio de la longitud natural del resorte. La energía potencial gravitatoria en la posición inicial te quedó

$U_i = mgd \sin \theta$

y en la posición final

$U_f = -mgx \sin \theta$

La variación de energía potencial gravitatoria entre estas posiciones es, por definición

$\Delta U_{i,f} = U_f - U_i = (-mgx \sin \theta) - (mgd \sin \theta) = - mg(d+x)\sin \theta$

que no es otra cosa que, aunque nombres algo distintos, 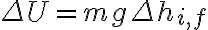$\Delta U = mg \Delta h_{i,f}$, siendo 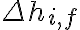$\Delta h_{i,f}$ el cambio total en la altura del cuerpo. La variación de energía potencial gravitatoria es negativa porque el cuerpo pasa de una altura mayor a una altura menor: tiene menor energía al final que al principio. Este es un resultado general para cualquier cuerpo que esté bajando (cuando un cuerpo aumenta su altura, la variación de energía potencial gravitatoria es positiva).

La energía potencial gravitatoria en este proceso se transforma primero en energía cinética y luego en energía potencial elástica, de manera que en todo momento del proceso la energía mecánica total es constante.

---

Espero haber podido ayudar a que se entienda. Te dejo una pregunta extra para reflexionar ahora sobre la energía potencial elástica. Según la ecuación 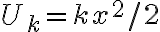$U_k=kx^2/2$, esta energía es positiva para cualquier 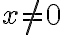$x\neq 0$. ¿Puede haber una variación negativa de energía potencial elástica? Si la respuesta es negativa, explica por qué, y si es afirmativa, explica cómo sería posible.

---

Suerte,
NC