Discusión y preguntas

La clase pasada del 03/04/25 surgió brevemente la duda de si acaso el carácter constructivo de (valga la redundancia) la construcción de los reales vista implicaría ciertas propiedades idóneas como que cualquier conjunto de reales resulte medible Lebesgue.

La motivación para una tal cuestión es clara: Según se nos enseña, aquellos conjuntos en un cierto sentido "patológicos" (a la Vitali) que rompen con la medibilidad Lebesgue son producto de un uso de 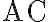$\mathsf{AC}$ (principio, claro está, de un carácter fuertemente no constructivo), lo cual nos llevaría a pensar que, quizá, extirpando el tal agente "no constructivo", uno podría por fin alcanzar esta medibilidad Lebesgue universal a través de $\mathcal{P}(\mathbb{R})$.

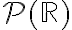Esta intuición resulta ser más bien un cierto prejuicio ya arraigado, pues si bien es cierto que la medibilidad Lebesgue universal de los (conjuntos de) reales es incompatible con 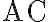$\mathsf{AC}$, este principio no es per se el causante de su falla a través de 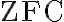$\mathsf{ZFC}$. En efecto, no es cierto que 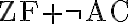$\mathsf{ZF} + \neg\mathsf{AC}$ pruebe tal cosa (llamémosle $\lambda(\mathcal{P}(\mathbb{R}))$).

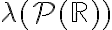A modo de ejemplo, es sabido que el Lema del Ultrafiltro (extensibilidad de cualquier filtro en un ultrafiltro y existencia de un ultrafiltro no trivial) es un principio de elección estrictamente más débil que 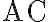$\mathsf{AC}$. No obstante, basta con asegurar la existencia de un ultrafiltro no trivial sobre $\omega$ para garantizar la existencia de ciertos conjuntos no medibles (sin por ello necesitar de una buena ordenación de $2^\omega$). 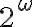Otro ejemplo posible sería el del teorema de Hahn-Banach, el cual puede verse también como un principio de elección que resulta implicar la existencia de un conjunto no medible Lebesgue (vid. este artículo por el excelente X. Caicedo).

Adicionalmente, a mediados de 1970, R. Solovay probó la existencia de un modelo de 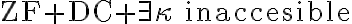$\mathsf{ZF} + \mathsf{DC} + \exists\kappa\text{ inaccesible}$ en que 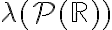$\lambda(\mathcal{P}(\mathbb{R}))$ se cumplía. El supuesto de existencia de un cardinal inaccesible podría quizá parecer fortuito o prescindible, pero unos años más tarde, en 1984, S. Shelah mostró que éste resultaba en verdad necesario, y que las dos teorías (i.e. 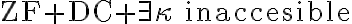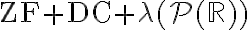$\mathsf{ZF} + \mathsf{DC} + \exists\kappa\text{ inaccesible}$ y $\mathsf{ZF} + \mathsf{DC} + \lambda(\mathcal{P}(\mathbb{R}))$) eran en verdad equiconsistentes. Este hecho apunta luego a que la mera ausencia de 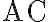$\mathsf{AC}$ no es garante suficiente para la medibilidad Lebesgue universal de todos los conjuntos de reales, sino que ésta requiere más bien de ciertos supuestos fuertes en la forma de cardinales grandes (hecho que a su vez sugiere que quizá haya un cierto carácter no constructivo escondido en la misma).

Esta sospecha se torna ahora cierta si examinamos la primera respuesta a este post realizado a través de MathOverflow. En efecto, 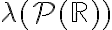$\lambda(\mathcal{P}(\mathbb{R}))$ resulta ser incompatible con cualquier teoría intuicionista/constructivamente aceptable en tanto que implica el principio (débil) del tercio excluso (i.e. 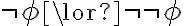$\neg\phi \lor \neg\neg\phi$ para cualquier 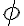$\phi$). (Según muestra el autor, si se asume además que la medida $\lambda : \mathcal{P}(\mathbb{R}) \to \mathbb{R}^+$ es tal que aquellos conjuntos con medida positiva no son vacíos, entonces obtenemos el tercio excluso completo.)

Como addendum, si bien es tenido por cierto que ninguna expresión "explícita" de un conjunto no medible Lebesgue (o de un buen ordenamiento de 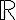$\mathbb{R}$) puede darse en 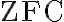$\mathsf{ZFC}$, vale la pena apreciar también que, en una teoría como 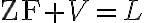$\mathsf{ZF} + V = L$, sí existen tales construcciones "explícitas" de los mismos.