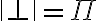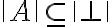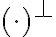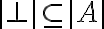Realizabilidad clásica. Oponentes de bottom.

Realizabilidad clásica. Oponentes de bottom.

de Juan Pablo García Garland -
Número de respuestas: 1

Tengo una duda muy concreta, que aclarándola me va a confirmar si estoy pensando bien:

Si tengo en el stack un oponente de una fórmula arbitraria A , digamos 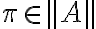 \pi \in ||A|| , puedo usarlo siempre como oponente de \bot , correcto?

Porque || \bot || = || \forall X. X|| = \cup || X [E / X] || = \cup || E ||.  Por tanto, el oponente de cualquier cosa, en particular de A va a estar en la unión de los oponentes de cualquier cosa. ¿Es Correcto?
En respuesta a Juan Pablo García Garland

Re: Realizabilidad clásica. Oponentes de bottom.

de Mauricio Guillermo -
Exacto: \|\bot\|=\Pi y por lo tanto \|A\|\subseteq \|\bot\| para toda fórmula A. Como (\cdot)^{\bot} es contravariante, entonces |\bot|\subseteq |A|, es decir, si realizas \bot, entonces realizas todas las fórmulas (lo que es coherente con el princpio "ex falso quodlibet").
Abrazo,
Mauricio.