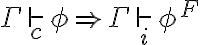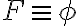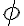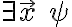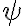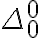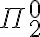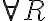IR: Duda sobre el truco de Friedman

Hola, hago la pregunta que surgió ayer:

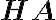En las notas (definición 6.3) dice que $R$ debe ser una "fresh propositional constant" o sea, un predicado de aridad 0 "fresco" (entiendo que esto simplemente significa que no puede ser ninguno de los predicados de aridad 0 que ya tenga nuestro lenguaje pero $\mathbf{HA}$ no tiene símbolos de predicado de aridad 0, no?)

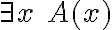Bien, aparte de eso, llegado el momento de hacer el "truco" se dice que la idea es cambiar $R$ por $\exists x\ A(x)$ , entonces mis dudas son 2:

¿Esto cuenta como un símbolo fresco?
Una vez introducimos 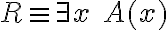$R \equiv \exists x\ A(x)$ en las fórmulas de 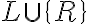$L\cup \{R\}$ vamos a pasar a tener 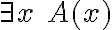$\exists x\ A(x)$ (la fórmula que se formo usando las reglas) y " 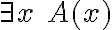$\exists x\ A(x)$ " (la fórmula que se formo porque $R$ es un predicado de aridad 0 y por lo tanto una fórmula). ¿Es así?
Si es así, ¿Cómo distinguimos esas dos fórmulas? Porque cuando por ejemplo (en el teorema 6.1) dice que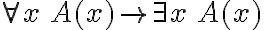 $\forall x\,A(x)\rightarrow \exists x\,A(x)$ la formula que en realidad tenemos es 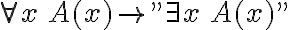$\forall x\,A(x)\rightarrow "\exists x\,A(x)"$ , ¿no?

Capaz tengo demasiado olvidado el tema de lenguajes de 1er orden, pero si introducimos $R$ como un predicado de aridad 0 en principio no podemos operar con el usando las reglas del existe y demás porque es solamente un chirimbolo, ¿no?

Espero haberme explicado.

Saludos,
Franco.

Re: Duda sobre el truco de Friedman

de Martin Jose Bula Sire - lunes, 31 de marzo de 2025, 14:35

Buenos días, Franco.

Creo que tu duda surge del hecho de que Streicher decide presentar la traducción (por doble negación) de Friedman (y el subsecuente "truco") en términos de un predicado nulario "fresco". Esto en sí no es necesario, y Friedman de hecho utiliza una "fórmula cualquiera" en su artículo original.

Lo esencial aquí es que, escogiendo una fórmula cualquiera (salvo ciertos cuidados respecto a variables libres y ligadas), puedes probar el Lema 6.3 (i.e. que

$\Gamma \vdash_c \phi \Rightarrow \Gamma \vdash_i \phi^F$ ). Esto implica, en particular, que, escogiendo

$F \equiv \phi$ cuando

$\phi$ es

$\Sigma_1^0$ (i.e. de la forma

$\exists \vec{x} \ \psi$ con

$\psi$

$\Delta_0^0$ *), podemos probar —intuicionísticamente—, como Streicher detalla, que

$\exists \vec{x} \ \psi$ , siempre que ésta valga de forma clásica (allí subyace el truco que Friedman emplea). Esto, claro está, nos permite también establecer lo mismo de las fórmulas

$\Pi_2^0$ , como más abajo se enuncia.

*Un caveat importante es que las tales fórmulas han de ser decidibles (condición, claro, que la

$\mathbf{HA}$ verifica).

Re: Duda sobre el truco de Friedman

de Mauricio Guillermo - viernes, 4 de abril de 2025, 21:25

Hola,

Complementando lo que dice Martín: el tema es que cuando en una demostración introduces una constante de predicado "fresca"

, en la prueba necesariamente no usaste nada especifico de esa constante. Entonces, tu prueba es --insistiendo en lo que creo que es la clave de todo esto-- uniforme en

Entonces, cuando cambies

$R$ por cualquier fórmula

$A$ en la prueba, todas las reglas se aplican. Comentaba yo que meter esa constante "fresca" es una manera de cuantificar en segundo orden sin meterlo formalmente en el lenguaje. En el fondo una expresión que depende de un

$R$ "fresco" dice algo que vale

$\forall R$ , pero no lo puedes escribir porque no te autorizas el cuantificador.

Saludos,

Mauricio.