Buenas tardes, quisiera que alguien me oriente respecto a si el razonamiento está bien realizado.
Buenos días Anntonella: el inicio de tu demostración tiene serios errores.
Para empezar, no se entiende la estrategia de la demostración. Aparentemente, tu intención es probar que la afirmación vale si reemplazas el exponente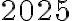 por cualquier exponente natural, pero no lo explicas ni tampoco enuncias una proposición que quieres demostrar.
por cualquier exponente natural, pero no lo explicas ni tampoco enuncias una proposición que quieres demostrar.
Entiendo que tu intención es definir la proposición abierta "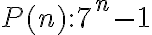 es múltiplo de
es múltiplo de 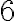 " y luego apuntas a probar que
" y luego apuntas a probar que 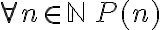 .
.
En tal caso, el enunciado del paso base es que "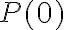 es cierta". Sin embargo, allí escribes algo distinto, y luego procedes a probar que
es cierta". Sin embargo, allí escribes algo distinto, y luego procedes a probar que 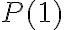 es cierta, lo que omite el primer natural y por tanto no vas a poder demostrar empleando el principio de inducción completa que
es cierta, lo que omite el primer natural y por tanto no vas a poder demostrar empleando el principio de inducción completa que 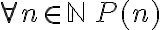 .
.
La demostración de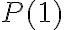 es errática y usas incorrectamente el conectivo de implicancia. Es al revés: quieres probar que
es errática y usas incorrectamente el conectivo de implicancia. Es al revés: quieres probar que 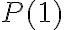 es cierta, por lo que no es correcto
es cierta, por lo que no es correcto
iniciar mencionando que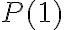 se cumple y luego hacer cuentas aparte.
se cumple y luego hacer cuentas aparte.
Por último, el enunciado y el planteo del paso inductivo no está bien ordenado. Al costado del enunciado dices que si es un número natural entonces
es un número natural entonces  es un número natural, lo que es falso.
es un número natural, lo que es falso.
Además, en la demostración del paso inductivo, el número que aparece en un exponente de pronto aparece multiplicando.
que aparece en un exponente de pronto aparece multiplicando.
Hay fallas atencionales, y otras que responden a la forma de la demostración. Para aprender a escribir demostraciones empleando el principio de inducción completa tienes que dedicar mucho tiempo de calidad, atendiendo a cada uno de los detalles y consignas que damos en el curso.
Te sugiero que asistas a clases y que te reúnas con tus compañeras/os para agilizar el aprendizaje.
Cordiales saludos,
Pablo.
Para empezar, no se entiende la estrategia de la demostración. Aparentemente, tu intención es probar que la afirmación vale si reemplazas el exponente
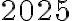 por cualquier exponente natural, pero no lo explicas ni tampoco enuncias una proposición que quieres demostrar.
por cualquier exponente natural, pero no lo explicas ni tampoco enuncias una proposición que quieres demostrar.Entiendo que tu intención es definir la proposición abierta "
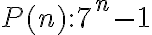 es múltiplo de
es múltiplo de  " y luego apuntas a probar que
" y luego apuntas a probar que 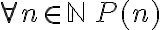 .
.En tal caso, el enunciado del paso base es que "
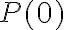 es cierta". Sin embargo, allí escribes algo distinto, y luego procedes a probar que
es cierta". Sin embargo, allí escribes algo distinto, y luego procedes a probar que 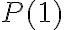 es cierta, lo que omite el primer natural y por tanto no vas a poder demostrar empleando el principio de inducción completa que
es cierta, lo que omite el primer natural y por tanto no vas a poder demostrar empleando el principio de inducción completa que 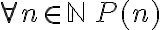 .
.La demostración de
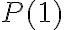 es errática y usas incorrectamente el conectivo de implicancia. Es al revés: quieres probar que
es errática y usas incorrectamente el conectivo de implicancia. Es al revés: quieres probar que 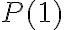 es cierta, por lo que no es correcto
es cierta, por lo que no es correcto iniciar mencionando que
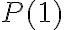 se cumple y luego hacer cuentas aparte.
se cumple y luego hacer cuentas aparte.Por último, el enunciado y el planteo del paso inductivo no está bien ordenado. Al costado del enunciado dices que si
 es un número natural entonces
es un número natural entonces  es un número natural, lo que es falso.
es un número natural, lo que es falso. Además, en la demostración del paso inductivo, el número
 que aparece en un exponente de pronto aparece multiplicando.
que aparece en un exponente de pronto aparece multiplicando.Hay fallas atencionales, y otras que responden a la forma de la demostración. Para aprender a escribir demostraciones empleando el principio de inducción completa tienes que dedicar mucho tiempo de calidad, atendiendo a cada uno de los detalles y consignas que damos en el curso.
Te sugiero que asistas a clases y que te reúnas con tus compañeras/os para agilizar el aprendizaje.
Cordiales saludos,
Pablo.
Hola, como están? Quisiera saber si mi ejercicio 7 tiene errores en la demostración. Gracias!

