La verdad no se como encararlo de forma inductiva
Hola Santiago, te tiro un pique:
Si tienes dos segmentos de recta, de longitud a y b, respectivamente, entonces siempre te puedes construir un segmento de longitud
(basta construir el triángulo rectángulo con catetos de longitud a y b). Esta observación te va a ser útil, ahora prosigamos con la inducción, primero tenemos que dejar bien en claro cual es la afirmación que queremos probar por inducción.
La afirmación es S(n): a partir de un segmento de longitud 1 usando regla y compás es posible construir un segmento de longitud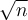
.
El paso base n=1 es trivial (¿por qué?).
Suponte que S(k) sea verdadera para todo k:
donde n es un entero positivo fijo (hipótesis inductiva) y trata de probar que S(n+1) es verdadera.
(traducido a segmentos es: si puedes construir segmentos de longitudes
entonces usando esos segmentos, con regla y compás puedes construir un segmento de longitud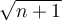 
).
Cualquier cosa si se te complica mucho subí una foto de donde te trancaste.
Saludos,
Claudio
Si tienes dos segmentos de recta, de longitud a y b, respectivamente, entonces siempre te puedes construir un segmento de longitud
(basta construir el triángulo rectángulo con catetos de longitud a y b). Esta observación te va a ser útil, ahora prosigamos con la inducción, primero tenemos que dejar bien en claro cual es la afirmación que queremos probar por inducción.La afirmación es S(n): a partir de un segmento de longitud 1 usando regla y compás es posible construir un segmento de longitud
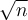.El paso base n=1 es trivial (¿por qué?).
Suponte que S(k) sea verdadera para todo k:
donde n es un entero positivo fijo (hipótesis inductiva) y trata de probar que S(n+1) es verdadera.(traducido a segmentos es: si puedes construir segmentos de longitudes
entonces usando esos segmentos, con regla y compás puedes construir un segmento de longitud 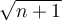). Cualquier cosa si se te complica mucho subí una foto de donde te trancaste.
Saludos,
Claudio
En respuesta a Santiago Sampol Morales
Re: Práctico 1-Ejercicio 10
Caso para n=1 es trivial. Para el caso para n=2, basta hacer un cuadrado de 1x1, su diagonal mide raíz de 2. Ahora, haciendo un rectángulo de lado 1 y largo raíz de 2, su diagonal mide raíz de 3 (probalo), a partir de ahí creo que podes ver el punto: Haciendo un rectángulo de lado Raíz de 3 y otro lado 1, su diagonal mide raíz de 4. c: ahora a demostrar por inducción asumiendo que podes construir un lado de raíz cuadrada de n.