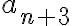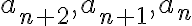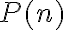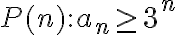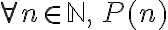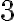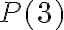Buenos días Guillermo: me alegra comprobar que, excepto por un error que con facilidad vas a poder corregir, el resto de tu demostración es correcta.
El principio de inducción completa se enuncia sobre una proposición abierta
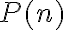
. En este caso, lo correcto es enunciar
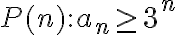
.
Una vez que completes tanto la demostración del paso base como del paso inductivo vas a poder emplear el principio de inducción fuerte
(con exactamente 3 pasos base tal como lo hiciste) y concluir que
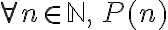
, que es precisamente lo que querías demostrar.
Es importante que notes que
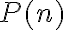
no es una proposición, puesto que yo no le puedo asignar un valor de verdad.
Sin embargo, sí es lo que llamamos una "proposición abierta", puesto que si me dices algún número natural concreto, digamos
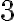
, yo te puedo decir si
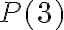
es verdadera o falsa (en este caso es verdadera).
Cordiales saludos,
Pablo.