Foro

Parametricé el elipsoide como:

$\phi \left(u,v\right)=\left(a \times \sin \left(u\right) \times \cos \left(v\right),b \times \sin \left(u\right) \times \sin \left(v\right),c \times \cos \left(u\right)\right)$

con u entre o y pi y v entre o y 2pi

Las derivadas parciales me quedaron:

$\frac{d}{du} \phi =\left(a \times \cos \left(u\right) \times \cos \left(v\right),b \times \cos \left(u\right) \times \sin \left(v\right),-\left(c\right) \times \sin \left(u\right)\right)$

$\frac{d}{dv} \phi =\left(-\left(a\right) \times \sin \left(u\right) \times \sin \left(v\right),b \times \sin \left(u\right) \times \sin \left(v\right),0\right)$

Usando el campo X = (x,0,0), y haciendo el producto mixto entre 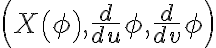$\left(X\left( \phi \right), \frac{d}{du} \phi , \frac{d}{dv} \phi \right)$

Me quedo a integrar $\int_{0}^{ \Pi } \int_{0}^{2 \cdot \Pi }abc \times \sin \left(u\right)^{3} \times \sin \left(v\right) \times \cos \left(v\right)\,du\,dv$

Que separando las integrales la de sen(v)cos(v) me da 0, porque es esto?