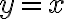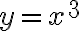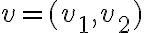Hola, este ejercicio pide estudiar la continuidad y luego las derivadas direccionales. Tengo dudas acerca del teórico y como estudiar una función partida.
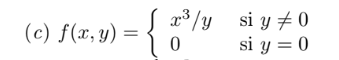
Sabemos que el punto critico es y=0, después en todo el dominio la función es diferenciable, y por lo tanto existen sus derivadas parciales/direccionales y además es continua.
¿Cómo hago para estudiar su continuidad en ese punto en varias variables? Porque entiendo que no basta con que los límites me den igual para demostrar que la función en ese punto es continua. Sin embargo, si dan diferente si sirve.
Se me ocurrió estudiar cuando y=x^3, que te queda x^3/x^3=1
Entonces ¿Es correcto decir que la función no es continua en y=0? porque los límites dan diferente.
Por otra parte, para estudiar la derivada direccional en (0,0) me basta con aplicar el limite y que me de igual a 0 para decir que existe?
Quedo expectante a una respuesta, saludos.