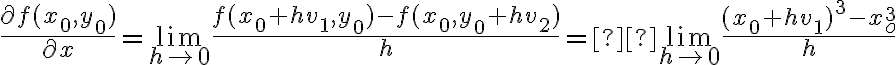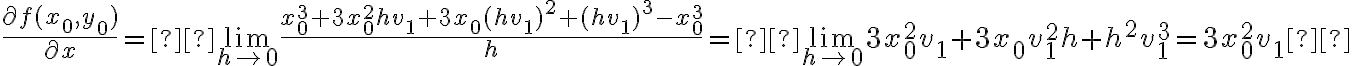Buenas, en la solución de este ejercicio dice que en la región en la que y=1 y x≠0, solo existen derivadas direcc. según (x,0) con x perteneciente a reales. Entiendo de dónde sale este cálculo, pero ¿No aplicaría también para las y>1 por la manera en que está dada la función? (Pues la derivada parcial según y de la función seguirá siendo 0 con y>1).
Es decir ¿No aplica esta solución para la región de los y>1 además del y=1?
Buenas!
En la región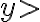 la función vale
la función vale 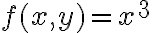 que posee derivadas direccionales en todo punto. Por las dudas lo probamos, nos fijamos un
que posee derivadas direccionales en todo punto. Por las dudas lo probamos, nos fijamos un 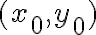 cualquiera en
cualquiera en 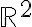 y
y 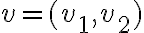 una dirección:
una dirección:
En la región
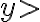 la función vale
la función vale 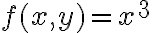 que posee derivadas direccionales en todo punto. Por las dudas lo probamos, nos fijamos un
que posee derivadas direccionales en todo punto. Por las dudas lo probamos, nos fijamos un 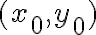 cualquiera en
cualquiera en 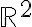 y
y 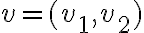 una dirección:
una dirección:Desarrollando el numerador del límite obtenemos:
La derivada parcial depende del punto 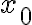 en el que me pare y de la componente
en el que me pare y de la componente 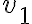 del vector dirección, pero existe en todo punto.
del vector dirección, pero existe en todo punto.
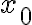 en el que me pare y de la componente
en el que me pare y de la componente 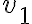 del vector dirección, pero existe en todo punto.
del vector dirección, pero existe en todo punto.Saludos!
Florencia
Bien, estaba confundido con el concepto de derivada direccional pero ya lo entendí, gracias.
Buenas, estaba leyendo este razonamiento y tengo una duda, haciendo este ejercicio me da lo mismo en este caso y en el caso en el que y=1 y x distinto de 0, por qué en la solución dice que depende de v1? Y no dice lo mismo en este caso de y mayor a 1.
Gracias
Gracias