Ejercicio 9

Ejercicio 9

de Mateo Roman Allonca Maldonado -
Número de respuestas: 2

Hola, tengo una duda de cómo realizar el límite por definición de una derivada parcial. Este es el ejercicio:


En la parte a), sabemos que existen las derivadas parciales en x 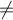 \neq 0 . Ahora para saber si se cumple también en x=0 tenemos que hacer el límite de la derivada parcial por definición. Hasta acá todo ok. 

Mi duda es la siguiente: para (0,yo) ¿Es correcto sustituir de ésta forma? Quedando el límite cuando h->0 de (h^2 + yo^2)sin(1/(h^2+yo^2))/h 
De esta forma nos queda que h+yo^2sin(1h^2+yo^2). Por lo tanto: yo^2 es una constante (un número real), la función sin está acotada en este caso y además h es 0. Por lo tanto el valor del límite da 0. ¿Es correcto plantearlo así? Me quedó la duda porque no entendí lo que propusieron en el apartado de soluciones del repartido 8. 

Quedo a la espera de una respuesta, saludos. 
En respuesta a Mateo Roman Allonca Maldonado

Re: Ejercicio 9

de Rafael Parra -
Hola Mateo, para la parte (a), puedes separar en dos casos.
  • (x_0,y_0)\neq (0,0), en este caso, puedes derivar la expresion  x²+y^2\sin( \frac{1}{x^2 +y^2} ) usando las reglas usuales de derivación y luego sustituir para obtener el valor de la derivada en ese punto. 
  • (x_0,y_0)= (0,0), en este caso, debes hacerlo por definicion. Por ejemplo la derivada parcial con respecto a x es el valor \lim_{h\to 0} \frac{f(0+h,0)-f(0,0)}{h}=\lim_{h\to 0} \frac{f(h,0)}{h}=\lim_{h\to 0}h\sin \frac{1}{h^2} =0

quedo atento si esto aclara tu duda

Saludos