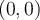CDIVV-2S: Derivadas parciales

buenas, yo tengo una duda que cre que es simple, para pribar que una funcion es diferenciable dicho rapidamente hay que primero ver si es continua la funcion en cierto punto dado, despues ver si existen las derivadas parciales y despues ver la definicion de diferenciabilidad y trabajar con el reto.
Mi pregunta viene en un caso especifico que es el siguiente: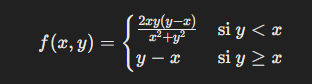

en un caso como este que el problema es la recta y=x que es donde para un lado hay una region y para otro lado la otra, si yo quiero trabajar en el punto (0,0) que pertenece a esa recta, la existencia de las derivadas parciales solo se hallan trabajando con la region que tiene el simbolo de menor o igual o tambien hay que ver en la otra por si esa variacion en x e y cambia a la otra region.
yo pienso que debido a que las derivads parciales se estudian localmente, solo hay que trabajar con la region de menor o igual, pero queria saber si este razonamiento es correcto.

Re: Derivadas parciales

de Mateo Musitelli - viernes, 25 de octubre de 2024, 09:03

Hola Joaquín, ¿cómo estás?

Lo importante, que tu lo mencionas, es comprender en qué punto estamos estudiando la diferenciabilidad,

$(0,0)$ en este caso.

Para determinarlo, puedes probar de dos maneras, en primer luger (cronológicamente figura así en las notas) estudiar:

$\lim_{(\Delta x, \Delta y)\to(0,0)} \frac{r(\Delta x, \Delta y)}{\sqrt{\Delta x ^2 + \Delta y ^2}}$

Si dicho límite existe, y vale cero, entonces la función es diferenciable en origen, siendo que aquí utilizaríamos

$f(a+h) = f(a) + df_a(h)+r(h)$ , con

$a = (0,0)$ y

$h=(\Delta x, \Delta y)$ .

Por otro lado, aplicando el Teorema 6.17 de las notas, donde la diferenciabilidad en

$a$ se de,uestra a partir de la continuidad de las derivadas parciales, también en

$a$ .

Quedo atento a si de este modo logras destrancarte y avanzar en el ejercicio.

Saludos,

M