Hola, en la solución dice que cuando y=1, x distinto de 0 solo existen las der. Direccionales según (lambda, 0) con lambda perteneciente a los reales. Pero no sería que las direcciones solo existen según (lambda, 1) con lambda perteneciente a los reales?
Hola Clementina,
La definición de derivada en la dirección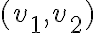 en un punto
en un punto 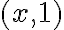 es el
es el  , por lo tanto si
, por lo tanto si 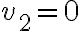 la primera evaluación de
la primera evaluación de  es sobre la recta
es sobre la recta 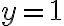 , y si
, y si 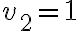 no lo es. Esto es que desde el pto
no lo es. Esto es que desde el pto 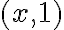 nos tenemos que mover por direcciones
nos tenemos que mover por direcciones 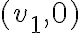 para permanecer en la recta
para permanecer en la recta 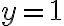 .
.
Para tener una idea geométrica, no hay que pensar al vector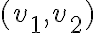 como un vector basado en el origen, sino como un vector con origen en el punto
como un vector basado en el origen, sino como un vector con origen en el punto 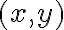 , donde queremos calcular la derivada direccional, y final en el punto
, donde queremos calcular la derivada direccional, y final en el punto 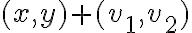 .
.
Cualquier cosa volvé a comentar nomás.
Saludos,
Leandro
La definición de derivada en la dirección
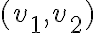 en un punto
en un punto 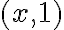 es el
es el  , por lo tanto si
, por lo tanto si 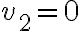 la primera evaluación de
la primera evaluación de  es sobre la recta
es sobre la recta 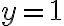 , y si
, y si 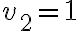 no lo es. Esto es que desde el pto
no lo es. Esto es que desde el pto 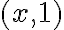 nos tenemos que mover por direcciones
nos tenemos que mover por direcciones 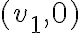 para permanecer en la recta
para permanecer en la recta 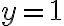 .
.Para tener una idea geométrica, no hay que pensar al vector
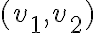 como un vector basado en el origen, sino como un vector con origen en el punto
como un vector basado en el origen, sino como un vector con origen en el punto 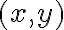 , donde queremos calcular la derivada direccional, y final en el punto
, donde queremos calcular la derivada direccional, y final en el punto 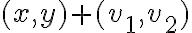 .
.Cualquier cosa volvé a comentar nomás.
Saludos,
Leandro
Buenas profe, cómo está?
Yo me tranque un poco con este ejercicio, no me doy cuenta de la existencia de las derivadas direccionales, le dejo abajo mi desarrollo, como podría seguir, o que debería hacer distinto?

Hola Emanuel, bien y vos?
Está perfecta la intención de separar entre qué sucede en la región superior a la recta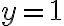 y qué sucede en la región inferior. El tema es que para evaluar no alcanza con saber solamente que
y qué sucede en la región inferior. El tema es que para evaluar no alcanza con saber solamente que 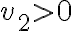 porque luego
porque luego  puede ser positivo o negativo, y eso hacer que el punto
puede ser positivo o negativo, y eso hacer que el punto 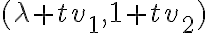 quede en una u otra región. Podemos asumir
quede en una u otra región. Podemos asumir 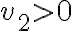 y el otro caso nos va a quedar análogo. Tenemos entonces que queremos calcular
y el otro caso nos va a quedar análogo. Tenemos entonces que queremos calcular 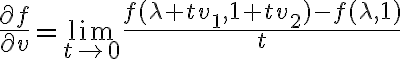 , y este límite existe si y solamente existen y son iguales los siguientes dos límites:
, y este límite existe si y solamente existen y son iguales los siguientes dos límites:
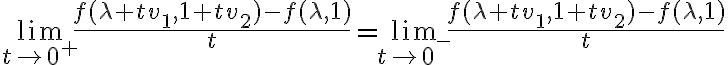
El primero de estos límites es:
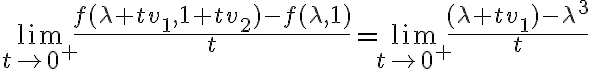
Al desarrollarlo nos va a quedar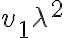 , porque en definitiva, estamos haciendo una derivada direccional en la región donde la función es
, porque en definitiva, estamos haciendo una derivada direccional en la región donde la función es 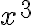 .
.
Luego hacemos lo mismo con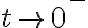 y vemos qué valores tienen que tener
y vemos qué valores tienen que tener 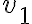 y
y 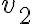 para que esos dos resultados coincidan.
para que esos dos resultados coincidan.
Fijate si con eso sale y sino volvé a consultar nomás con lo que te tranques o genere alguna duda.
Saludos,
Leandro
Está perfecta la intención de separar entre qué sucede en la región superior a la recta
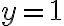 y qué sucede en la región inferior. El tema es que para evaluar no alcanza con saber solamente que
y qué sucede en la región inferior. El tema es que para evaluar no alcanza con saber solamente que 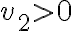 porque luego
porque luego  puede ser positivo o negativo, y eso hacer que el punto
puede ser positivo o negativo, y eso hacer que el punto 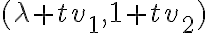 quede en una u otra región. Podemos asumir
quede en una u otra región. Podemos asumir 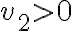 y el otro caso nos va a quedar análogo. Tenemos entonces que queremos calcular
y el otro caso nos va a quedar análogo. Tenemos entonces que queremos calcular 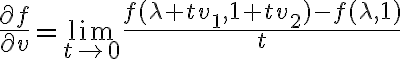 , y este límite existe si y solamente existen y son iguales los siguientes dos límites:
, y este límite existe si y solamente existen y son iguales los siguientes dos límites: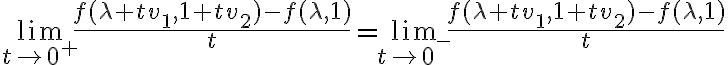
El primero de estos límites es:
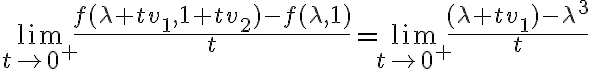
Al desarrollarlo nos va a quedar
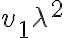 , porque en definitiva, estamos haciendo una derivada direccional en la región donde la función es
, porque en definitiva, estamos haciendo una derivada direccional en la región donde la función es 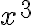 .
.Luego hacemos lo mismo con
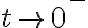 y vemos qué valores tienen que tener
y vemos qué valores tienen que tener 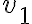 y
y 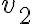 para que esos dos resultados coincidan.
para que esos dos resultados coincidan.Fijate si con eso sale y sino volvé a consultar nomás con lo que te tranques o genere alguna duda.
Saludos,
Leandro
Buenas, queria consultar sobre los limites mencionados:
En el caso que t tiende a cero +, me quedo que el limite es 3(𝜆^2)v1 no v1(𝜆^2).
Luego, el caso que t tiende a cero menos, el limite me quedo 0 (luego de desarrollar las potencias se me anulan todos los términos con t y me queda x^3-x^3 en el numerador por lo que es 0/t=0).
Al igualar estas condiciones deduci que v1 debe ser cero, por lo que solo existirian las derivadas direccionales del tipo v=(0,v2). Sin embargo, en las soluciones dice que solo existen las derivadas cuando v= (v,0) y no entiendo porque.
En el caso que t tiende a cero +, me quedo que el limite es 3(𝜆^2)v1 no v1(𝜆^2).
Luego, el caso que t tiende a cero menos, el limite me quedo 0 (luego de desarrollar las potencias se me anulan todos los términos con t y me queda x^3-x^3 en el numerador por lo que es 0/t=0).
Al igualar estas condiciones deduci que v1 debe ser cero, por lo que solo existirian las derivadas direccionales del tipo v=(0,v2). Sin embargo, en las soluciones dice que solo existen las derivadas cuando v= (v,0) y no entiendo porque.
Hola Josefina,
En el caso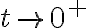 me comí el
me comí el 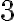 sí. En el otro caso, los términos de orden
sí. En el otro caso, los términos de orden  en
en  del denominador no quedan
del denominador no quedan  en el límite, porque se cancela con la
en el límite, porque se cancela con la  que está dividiendo. El resultado de ese límite es
que está dividiendo. El resultado de ese límite es 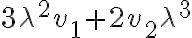 si no me equivoco. Cuando tenés un cociente donde tanto nominador como denominador tienen a
si no me equivoco. Cuando tenés un cociente donde tanto nominador como denominador tienen a  , tenemos una indeterminación y hay que resolverla, en este caso cancelando la
, tenemos una indeterminación y hay que resolverla, en este caso cancelando la  en los distintos sumandos. Un ejemplo concreto de ese tipo de error es con el límite de
en los distintos sumandos. Un ejemplo concreto de ese tipo de error es con el límite de 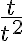 , que si hicieramos ese procedimiento el límite nos daría
, que si hicieramos ese procedimiento el límite nos daría  , pero no existe.
, pero no existe.
Saludos,
Leandro
En el caso
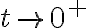 me comí el
me comí el 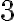 sí. En el otro caso, los términos de orden
sí. En el otro caso, los términos de orden  en
en  del denominador no quedan
del denominador no quedan  en el límite, porque se cancela con la
en el límite, porque se cancela con la  que está dividiendo. El resultado de ese límite es
que está dividiendo. El resultado de ese límite es 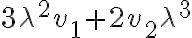 si no me equivoco. Cuando tenés un cociente donde tanto nominador como denominador tienen a
si no me equivoco. Cuando tenés un cociente donde tanto nominador como denominador tienen a  , tenemos una indeterminación y hay que resolverla, en este caso cancelando la
, tenemos una indeterminación y hay que resolverla, en este caso cancelando la  en los distintos sumandos. Un ejemplo concreto de ese tipo de error es con el límite de
en los distintos sumandos. Un ejemplo concreto de ese tipo de error es con el límite de 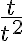 , que si hicieramos ese procedimiento el límite nos daría
, que si hicieramos ese procedimiento el límite nos daría  , pero no existe.
, pero no existe. Saludos,
Leandro
