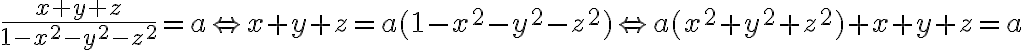Buenas noches,
Estoy tratando de encontrar el conjunto de nivel de la funcion f(x,y,z)=x+y+z/(1-x^2-y^2-z^2) y llego a que el conjunto de nivel es una esfera trasladada 1/a del origen. Pero no se de donde salen los valores de la solucion.

Buenas noches,
Estoy tratando de encontrar el conjunto de nivel de la funcion f(x,y,z)=x+y+z/(1-x^2-y^2-z^2) y llego a que el conjunto de nivel es una esfera trasladada 1/a del origen. Pero no se de donde salen los valores de la solucion.

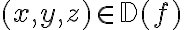 :
: