Buenas no entiendo la solución al siguiente problema:

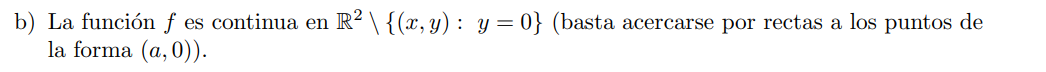
Traté de razonarlo como en la parte 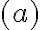 pero tomándome
pero tomándome 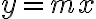 y evaluar
y evaluar 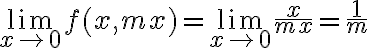 entonces supuse que, si depende de
entonces supuse que, si depende de 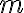 , el
, el 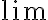 no existe pero creo que viendo la solución no es por ese lado.
no existe pero creo que viendo la solución no es por ese lado.
 . La idea es ver que pasa en un punto
. La idea es ver que pasa en un punto 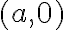 con
con  genérico. Una forma de escribir las rectas que pasan por
genérico. Una forma de escribir las rectas que pasan por 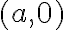 es de la forma
es de la forma 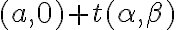 , donde
, donde 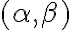 es la dirección de la recta por la que nos estamos acercando. Entonces los límites direccionales nos quedan
es la dirección de la recta por la que nos estamos acercando. Entonces los límites direccionales nos quedan 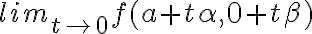 . Una recomendación para ayudar a entenderlo sería representar gráficamente esto para un punto, una dirección y su correspondiente recta.
. Una recomendación para ayudar a entenderlo sería representar gráficamente esto para un punto, una dirección y su correspondiente recta.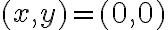 la función vale
la función vale  , mientras que en
, mientras que en 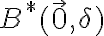 la función vale
la función vale 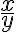 .
. cualquiera, por ello se sugiere el estudio del límite cuando
cualquiera, por ello se sugiere el estudio del límite cuando 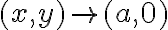 .
.