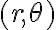Hola buenas, tenia una consulta sobre la interpretación de los incisos.
Por lo que entendí, la parte a) lo que quiere probar es la equivalencia que hay entre la existencia del límite en polares y en la definición que dimos en clase, PARA TODO TITA. Osea, que si demostras que el limite para todo tita es L, entonces se verifica la noción de límite que conocemos. Con esta interpretación, demostrando que el límite no depende de la dirección por la cual me acerque, podría afirmar la existencia del límite y calcularlo.
Ahora, el inciso 2 es para un tita fijo, osea tita=pi por ejemplo. Entonces, si existe el límite, necesariamente va a existir el límite en coordenadas polares, pero ahí el recíproco no es cierto porque puede existir pero depender de tita, y ahí no podríamos afirmar que el limite es L ya que depende de la dirección.
La duda es básicamente si el razonamiento es correcto o le estoy errando algo, porque me han dicho que coordenadas polares no sirve para afirmar nada, pero entonces no entiendo lo que quiere decir la parte a) del ejercicio.
Saludos y muchas gracias