Hola, Federica y Antonela
El sistema total no configura un rígido, por lo que no tiene definido una velocidad angular.
Si miramos sus partes, tenemos una barra, que rota en un sistema absoluto según la coordenada (definido según una dirección absoluta). Por tanto su velocidad angular es
(definido según una dirección absoluta). Por tanto su velocidad angular es 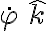 .
.
Por otro lado, el disco está rotando con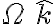 .
.
Si el ángulo estuviera definido con respecto a una dirección relativa al disco, entonces ahí sí aplicaría el teorema de adición de velocidades angulares. Esta opción es una decisión válida, pero no la que se adopta en la solución.
estuviera definido con respecto a una dirección relativa al disco, entonces ahí sí aplicaría el teorema de adición de velocidades angulares. Esta opción es una decisión válida, pero no la que se adopta en la solución.
Con respecto al sentido de la fuerza de rozamiento, por cómo es el sistema, el disco "empuja" a la barra a moverse en el mismo sentido que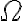 . De hecho la barra se encuentra inicialmente en reposo, por lo que el sentido de la fuerza de fricción dinámica tiene que ser hacia $+\hat{e}_{\varphi}$. Para verlo más intuitivo pensá en que pasaría si la barra se quedara quieta, ¿para donde apuntaría el rozamiento dinámico en ese caso?
. De hecho la barra se encuentra inicialmente en reposo, por lo que el sentido de la fuerza de fricción dinámica tiene que ser hacia $+\hat{e}_{\varphi}$. Para verlo más intuitivo pensá en que pasaría si la barra se quedara quieta, ¿para donde apuntaría el rozamiento dinámico en ese caso?
Saludos
El sistema total no configura un rígido, por lo que no tiene definido una velocidad angular.
Si miramos sus partes, tenemos una barra, que rota en un sistema absoluto según la coordenada
 (definido según una dirección absoluta). Por tanto su velocidad angular es
(definido según una dirección absoluta). Por tanto su velocidad angular es 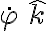 .
.Por otro lado, el disco está rotando con
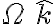 .
. Si el ángulo
 estuviera definido con respecto a una dirección relativa al disco, entonces ahí sí aplicaría el teorema de adición de velocidades angulares. Esta opción es una decisión válida, pero no la que se adopta en la solución.
estuviera definido con respecto a una dirección relativa al disco, entonces ahí sí aplicaría el teorema de adición de velocidades angulares. Esta opción es una decisión válida, pero no la que se adopta en la solución.Con respecto al sentido de la fuerza de rozamiento, por cómo es el sistema, el disco "empuja" a la barra a moverse en el mismo sentido que
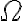 . De hecho la barra se encuentra inicialmente en reposo, por lo que el sentido de la fuerza de fricción dinámica tiene que ser hacia $+\hat{e}_{\varphi}$. Para verlo más intuitivo pensá en que pasaría si la barra se quedara quieta, ¿para donde apuntaría el rozamiento dinámico en ese caso?
. De hecho la barra se encuentra inicialmente en reposo, por lo que el sentido de la fuerza de fricción dinámica tiene que ser hacia $+\hat{e}_{\varphi}$. Para verlo más intuitivo pensá en que pasaría si la barra se quedara quieta, ¿para donde apuntaría el rozamiento dinámico en ese caso?Saludos
