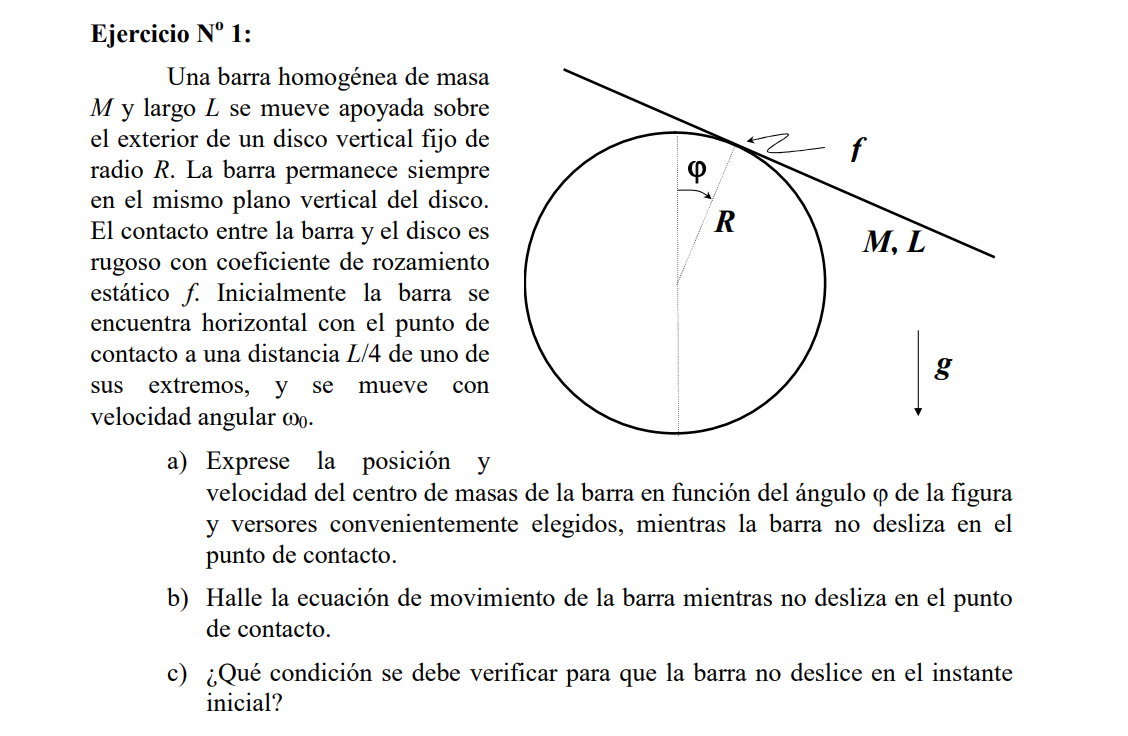
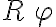Buenas, no entiendo porqué en la parte (a) en las soluciones la distancia |AI| es considerada L/4 + Rphi ya que la parte a dice que no se desliza del punto de contacto entonces a mi entender la distancia al borde de la barra seguiría siendo la inicial que es L/4. Adjunto el ejercicio y la parte de la solución a la que me refiero. Gracias.