Consultas de pruebas anteriores

Buenas

Efectivamente esa es la idea.

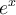Si intentas realizar el cambio $e^{x} = u$ the falta un $e^{x}$, por lo que hay que multiplicar y dividir, es decir

$\displaystyle \int_{1}^{3} \frac{dx}{e^x + 2} = \int_{1}^{3} \frac{e^x dx}{e^{x}(e^x + 2)} = \int_{e}^{e^{3}} \frac{du}{u(u+2)}$

La integral que te queda puedes resolverla con fracciones simples

Si tienes dudas de esto ultimo, u algún otro detalle vuelve a escribir

Saludos