Buenas
Vamos ejercicio por ejercicio
VF 1 - Ser creciente no implica derivabilidad. Puedes tomar por ejemplo funciones parttidas
ninguna de ellas es derivable en 0, pero ambas son estrictamente creciente
VF 2 - Es el teorema de Weierstrass (teorema 95 de las nota) Tambien esta en las clases de openfing y hay un video en la seccion guias y otrs materiales del tema 3
VF - 4 - La funcion valor absoluto tiene un mínimoo relativo (que además es absoluto) en 0, pero no es derivable. Lo que si vale es que si f ES derivable en un extremo relativo entonces la derivada tiene que ser 0, pero la funcion f no tiene por que ser derivable.
MO 1 - Los ejercicios con funciones partidas para las cuales te piden derivabilidad pueden ser complicados. En este caso es claro que  es derivable en
es derivable en 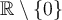 , es decir que solo nos falta estudiar la derivabilidad en 0. Para ello debemos de verificar 2 cosas - que sea continua en el punto y que las derivadas laterales sean iguales. la funcion
, es decir que solo nos falta estudiar la derivabilidad en 0. Para ello debemos de verificar 2 cosas - que sea continua en el punto y que las derivadas laterales sean iguales. la funcion  va a ser derivable si y solo si se cumplen estas dos cosas.
va a ser derivable si y solo si se cumplen estas dos cosas.
En este ejercicio, para estudiar la continuidad estudiamos los limite laterales de  en 0 asi como su evaluacion. Es decir tiene que cumplirse que
en 0 asi como su evaluacion. Es decir tiene que cumplirse que
En este caso
Es decir que para que f sea continua se tiene que cumplir que 
Realizando ahora el estudio de las derivadas laterales. En este caso, como las expresiones de ambas partes son derivables con derivadas continuas puedes igualar las derivadas de ambas expresiones [es decir 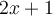 y
y  ]. Pero en general debes estudiar las derivadas laterales.
]. Pero en general debes estudiar las derivadas laterales.
tienes entonces que para que sea derivable (una vez que tenemos que es continua) se debe verificar que 
Si bien ya esta escalerizado, este es un sistema linea de 2 por 2 por lo que puedes determinar los valores de  y
y 
Saludos




