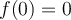Buen dia,
Al intentar resolver el ejercicio mediante polinomio de taylor me dio que a = 0 y b = -⅙(la opción b) pero las soluciones del parcial dice q es la opción c, por lo que intente volver a resolverlo mediante L'hopital y me volvio a dar a = 0 y b = -⅙