
hola, no se me ocurre como demostrar la parte b y c de este ejercicio

hola, no se me ocurre como demostrar la parte b y c de este ejercicio
Buenas
La idea es usar la parte a. Voy a plantear las ideas a grandes rasgos, si no te resultan suficientes vuelve a escribir
Sabemos que  con
con  . Supongamos que
. Supongamos que  , el otro caso es análogo.
, el otro caso es análogo.
Por continuidad existe 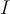 un entorno de
un entorno de  para el cual
para el cual 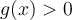 . luego el signo de f(x) es el signo de
. luego el signo de f(x) es el signo de  en ese entorno.
en ese entorno.
Si  es par, tendrás que
es par, tendrás que 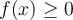 para todo
para todo 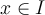 y como
y como  ,
,  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
Si  es impar
es impar  cambiara de signo, más precisamente
cambiara de signo, más precisamente 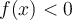 si
si  ,
, 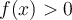 si
si  por lo que
por lo que  no puede tener un extremo relativo en
no puede tener un extremo relativo en  .
.
Cualquier cosa vuelve a escribir
Saludos