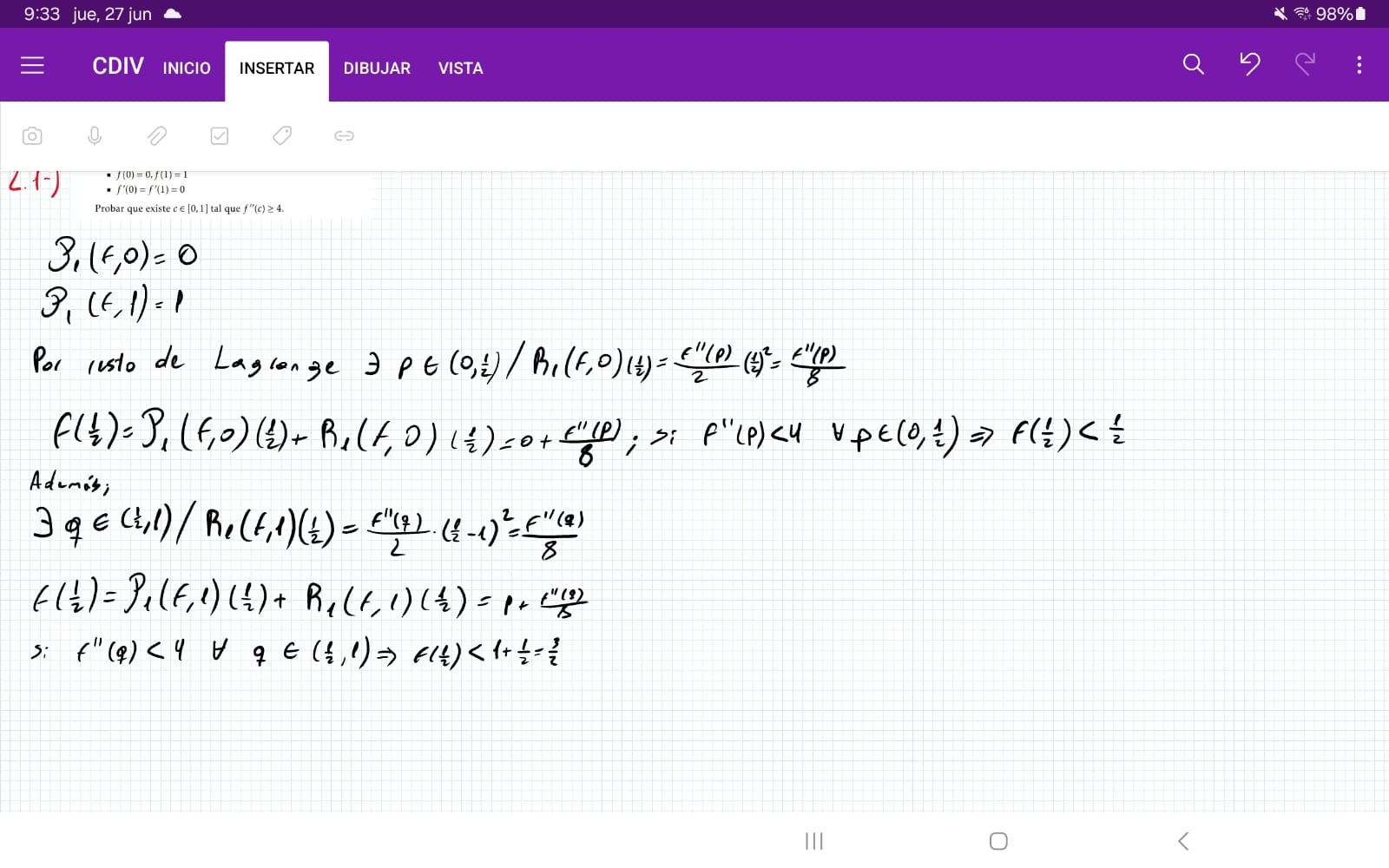
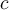Hola, estaba haciendo el ejercicio pero f"(c) me queda igual a 2 en vez de menor a 4, no me doy cuenta que estoy razonando mal
hola, también tengo dudas con este ejercicio
Buenas
La idea es escribir el polinomio de grado 1 junto con el resto
Por ejemplo, tomando el polinomio de Taylor de grado 1 en 0 tenemos que:
En particular, si evaluamos en 
Si planteas lo mismo desde  obtendrás la otra desigualdad y llegaras a un absurdo
obtendrás la otra desigualdad y llegaras a un absurdo
Si no pueden llegar a la conclusión vuelvan a escribir y planteamos el resto
Saludos
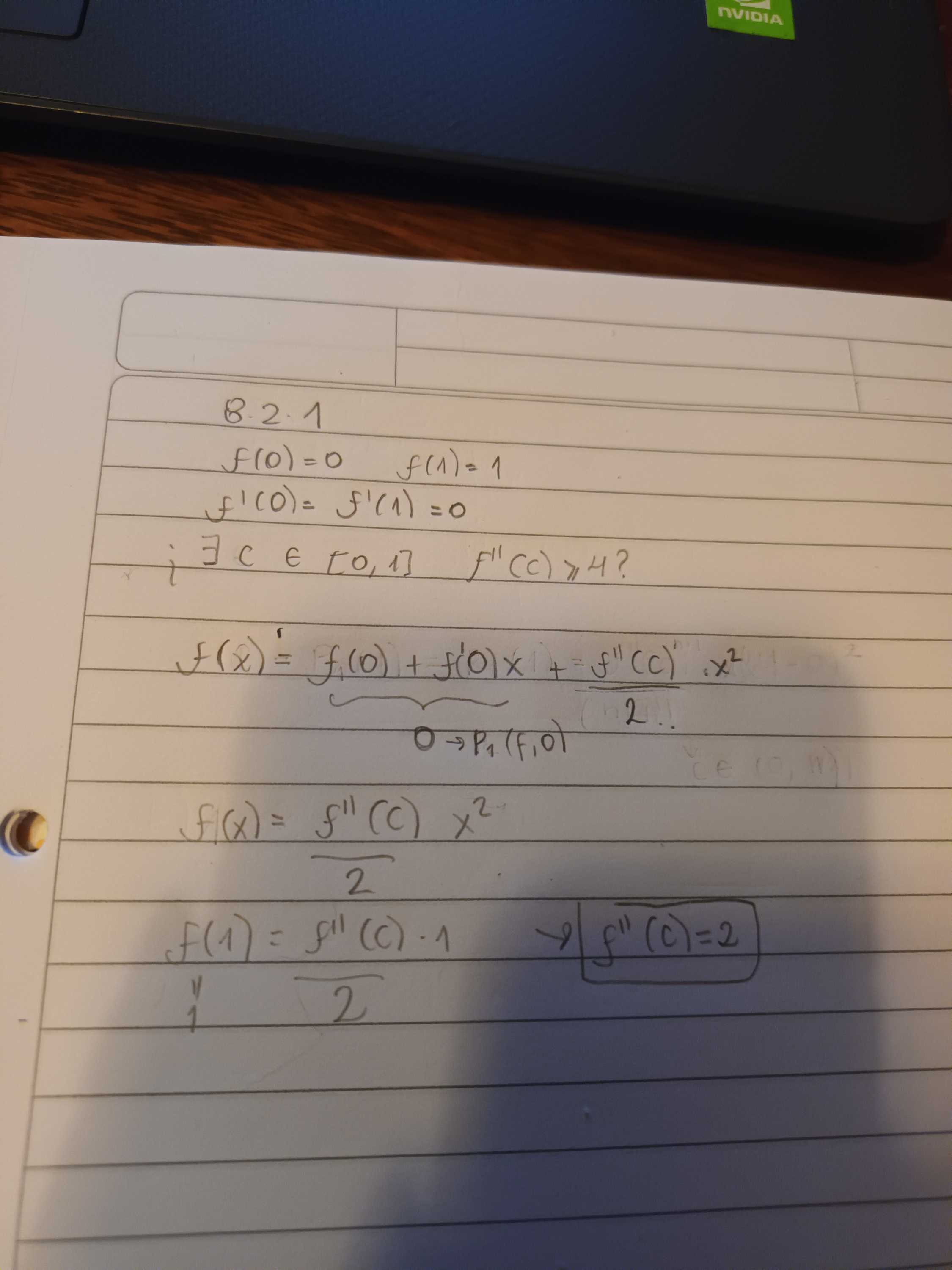
![c \in [0,x] c \in [0,x]](https://eva.fing.edu.uy/filter/tex/pix.php/fdd67bb7a0522ba201dc4a6ced2fb754.png)


![c \in [0,\frac{1}{2}] c \in [0,\frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/3120ecb56a4da8cb0b89a370e2753b14.png)