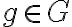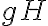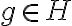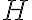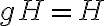Buenas, estaba viendo las notas sobre este tema y no me queda del todo claro esta última parte
Dado que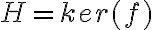 
, esto no implicaría que la condición 
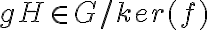es equivalente a simplemente 
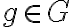, por lo cual 
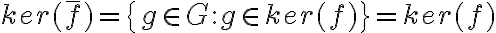, comprendo que lo que puse no puede ser correcto porque 
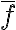toma conjuntos laterales y 
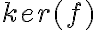tiene elementos de 
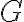, pero no me logro dar cuenta donde está el error, muchas gracias.
Estoy de acuerdo con tu idea. Y también con que formalmente no tiene sentido, porque los elementos del núcleo de deben ser clases laterales, y no elementos de .
En tu razonamiento estás identificando un elemento 
con su clase lateral 
. Esto es lo que hace la proyección canónica que aparece en el teorema. Creo que es una identificación tan natural que puede llevar a este tipo de confusión. Pero formalmente 
y deben considerarse como distintos (aunque estén relacionados).
Eso es lo que te puedo decir. Capaz algún otro docente te puede aportar otra forma de verlo.
Por otro lado, comento por si no está claro, que en el remate de la prueba lo que se usa es que la clase lateral de cualquier elemento 
es el propio conjunto 
. Es decir: si , entonces 
. Eso vale siempre, para cualquier subgrupo .
Saludos.