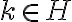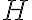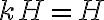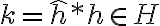Hola, buenas noches.
Repasando y leyendo las notas de subgrupos normales, no me quedó muy claro una cosa. En la página 15 se comienza la demostración de que si un conjunto cociente es invariante, entonces la operación del grupo cociente inducido está bien definida. Después del desarrollo, llegan a la siguiente expresión:
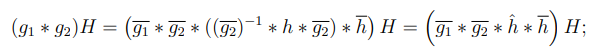
Seguido de lo siguiente: "(...) donde para la última igualdad definimos 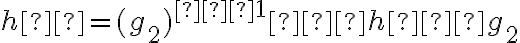 . Para finalizar, basta con probar
que
. Para finalizar, basta con probar
que 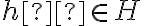 ; pues esto implica que
; pues esto implica que 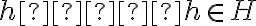 , lo cual a su vez implica que
, lo cual a su vez implica que 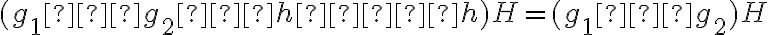 ..."
..."
Mi pregunta es, ¿por qué si 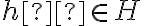 entonces vale
entonces vale 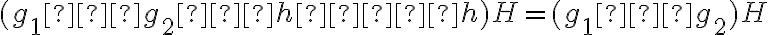 ? Me perdí un poco ahí.
? Me perdí un poco ahí.